Cho hai mặt phẳng: (P1): 2x + y + 2z + 1 = 0 và (P2): 4x – 2y – 4z + 7 = 0. Lập phương trình mặt phẳng

Câu hỏi và bài tập chương 3

Bài 3.53 trang 133 Sách bài tập Hình học 12: Cho hai mặt phẳng:

(P₁): 2x + y + 2z + 1 = 0 và (P₂): 4x – 2y – 4z + 7 = 0.

Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến (P₁) và (P₂) là bằng nhau.

Lời giải:

Ta có: M(x, y, z) ∈ (P) ⇔ d(M, (P₁)) = d(M, (P₂))

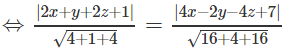
⇔ 2|2x + y + 2z + 1| = |4x − 2y − 4z + 7|

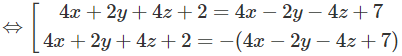
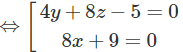
Từ đó suy ra phương trình mặt phẳng phải tìm là: 4y + 8z – 5 = 0 hoặc 8x + 9 = 0