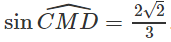Tính sin của góc tạo bởi hai mặt kề nhau (tức là hai mặt có một cạnh chung) của một tứ diện đều
Bài 2: Khối đa diện lồi và khối đa diện đều
Bài 1.6 trang 12 Sách bài tập Hình học 12: Tính sin của góc tạo bởi hai mặt kề nhau (tức là hai mặt có một cạnh chung) của một tứ diện đều.
Lời giải:
Cho tứ diện đều ABCD cạnh bằng a. Gọi M và N theo thứ tự là trung điểm của AB và CD. Khi đó góc giữa hai mặt (CAB) và (DAB) bằng ∠CMD = 2∠CMN
Ta có:
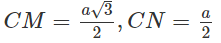
Do đó:
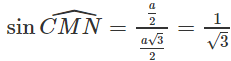
Từ đó suy ra: