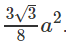Cho khối bát diện đều ABCDEF (h.1.9). Gọi O là giao điểm của AC và BD, M và N theo thứ tự là trung điểm

Bài 2: Khối đa diện lồi và khối đa diện đều

Bài 1.9 trang 12 Sách bài tập Hình học 12: Cho khối bát diện đều ABCDEF (h.1.9). Gọi O là giao điểm của AC và BD, M và N theo thứ tự là trung điểm của AB và AE. Tính diện tích thiết diện tạo bởi khối bát diện đó và mặt phẳng (OMN).

Lời giải:

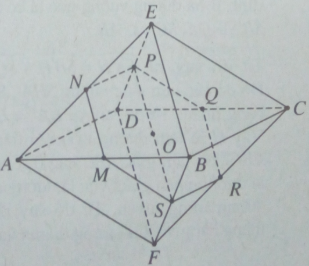
Ta có khối bát diện đều ABCDEF, cạnh a. Do MN // (DEBF) nên giao của mặt phẳng (OMN) với mặt phẳng (DEBF) là đường thẳng qua O và song song với MN.

Ta nhận thấy đường thẳng này cắt DE và BF tại các trung điểm P và S tương ứng của chúng. Do mặt phẳng (ADE) song song với mặt phẳng (BCF) nên (OMN) cắt (BCF) theo giao tuyến qua S và song song với NP. Dễ thấy giao tuyến này cắt FC tại trung điểm R của nó. Tương tự, (OMN) cắt DC tại trung điểm Q của nó. Từ đó suy ra thiết diện tạo bởi hình bát diện đã cho với mặt phẳng (OMN) là lục giác đều có cạnh bằng a/2.

Do đó diện tích của nó bằng