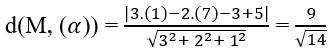Bài tập trắc nghiệm trang 135, 136, 137, 138, 139 Sách bài tập Hình học 12
Câu hỏi trắc nghiệm chương 3
Bài tập trắc nghiệm trang 135, 136, 137, 138, 139 Sách bài tập Hình học 12:
Các bài tập dưới đây cho trong không gian Oxyz
Bài 3.68: Cho mặt phẳng (α) đi qua hai điểm E(4; -1; 1), F(3; 1; -1) và song song với trục Ox. Phương trình tổng quát của (α) là:
A. x + y = 0 B. y + z = 0
C. x + y + z = 0 D. x + z = 0
Bài 3.69: Gọi (α) là mặt phẳng đi qua hai điểm A(1; 2; 3) và song song với mặt phẳng (β): x - 4y + z + 12 = 0. Phương trình tổng quát của (α) là:
A. x - 4y + z + 4 = 0 B. x - 4y + z - 4 = 0
C. x - 4y + z - 12 = 0 D. x - 4y + z + 3 = 0
Bài 3.70: Cho điểm I(2; 6; -3) và các mặt phẳng:
(α): x - 2 = 0
(β): y - 6 = 0
(γ): z + 3 = 0
Khẳng định nào sau đây là sai?
A. (α) đi qua I B. (β) // (xOz)
C. (γ) // Oz D. (α) ⊥ (β)
Bài 3.71: Phương trình của mặt phẳng chứa Oy và điểm Q(1; 4; -3) là:
A. 3x + z = 0 B. x + 3z = 0
C. 3x + y = 0 D. 3x - z = 0
Bài 3.72: Cho mặt phẳng (α): 2y + z = 0. Khẳng định nào sau đây là đúng?
A. (α) // Ox B. (α) // Oy
C. (α) // (yOz) D. (α) ⊃ Ox.
Bài 3.73: Cho ba điểm A(2; 1; -1), B(-1; 0; 4), C(0; -2; -1). Phương trình của mặt phẳng đi qua điểm A và vuông góc với đường thẳng BC là:
A. x - 2y - 5z + 5 = 0 B. x - 2y - 5z - 5 = 0
C. x - 2y - 5z = 0 D. 2x - y + 5z - 5 = 0
Bài 3.74: Gọi (γ) là mặt phẳng đi qua điểm M(3; -1; -5) và vuông góc với hai mặt phẳng: (α): 3x - 2y + 2z + 7 = 0, (β): 5x - 4y + 3z + 1 = 0.
Phương trình tổng quát của (γ) là:
A. 2x + y - 2z - 15 = 0 B. 2x + y - 2z + 15 = 0
C. x + y + z + 3 = 0 D. 2x + y - 2z - 16 = 0
Bài 3.75: Cho đường thẳng d có phương trình tham số:
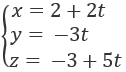
Phương trình chính tắc của d là:
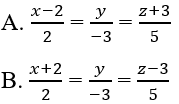
C. x - 2 = y = z + 3
D. x + 2 = y = z - 3
Bài 3.76: Cho đường thẳng d có phương trình tham số:
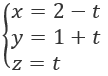
Phương trình chính tắc của d là:
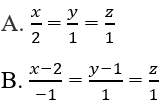
C. 2x + y + z - 5 = 0
D. x + y + z - 3 = 0
Bài 3.77: Phương trình chính tắc của đường thẳng đi qua hai điểm A(1; 2; -3) và B(3; -1; 1) là:
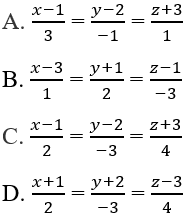
Bài 3.78: Tọa độ giao điểm M của đường thẳng d và mặt phẳng (α): 3x + 5y - z - 2 = 0 là:
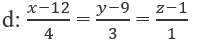
A. (1; 0; 1) B. (0; 0; -2)
C. (1; 1; 6) D. (12; 9; 1)
Bài 3.79: Cho đường thẳng d và mặt phẳng (α): x + 3y + z + 1 = 0
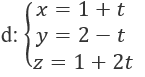
Khẳng định nào sau đây là đúng?
A. d // (α) B. d cắt (α)
C. d ⊂ (α) D. d ⊥ (α)
Bài 3.80: Cho đường thẳng d và mặt phẳng (α): x + y + z - 4 = 0
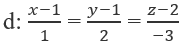
Khẳng định nào sau đây là đúng?
A. d cắt (α) B. d // (α)
C. d ⊂ (α) D. d ⊥ (α)
Bài 3.81: Hãy tìm kết luận đúng về vị trí tương đối giữa hai đường thẳng:
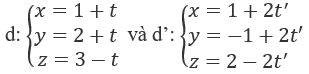
A. d cắt d' B. d ≡ d'
C. d chéo với d' D. d // d'
Bài 3.82: Giao điểm giữa hai đường thẳng:
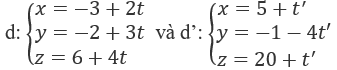
A. (-3; -2; 6) B. (5; -1; 20)
C. (3; 7; 18) D. (3; -2; 1)
Bài 3.83: Tìm m để hai đường thẳng sau đây cắt nhau:
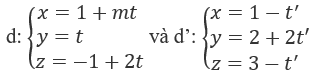
A. m = 0 B. m = 1
C. m = -1 D. m = 2
Bài 3.84: Khoảng cách từ điểm M(-2; -4; 3) đến mặt phẳng (α): 2x - y + 2z - 3 = 0 là:
A. 3 B. 2
C. 1 D. 11
Bài 3.85: Gọi H là hình chiếu vuông góc của điểm A(2; -1; -1) đến mặt phẳng (α): 16x - 12y - 15z - 4 = 0. Độ dài của đoạn AH là:
A. 55 B. 11/5
C. 11/25 D. 22/5
Bài 3.86: Cho mặt cầu tâm I(4; 2; -2) bán kính r tiếp xúc với mặt phẳng (P): 12x - 5z - 19 = 0. Bán kính r bằng:
A. 39 B. 3
C. 13 D. 39/√(13)
Bài 3.87: Cho hai mặt phẳng song song:
(α): x + y - z + 5 = 0
và (β): 2x + 2y - 2z + 3 = 0
Khoảng cách giữa (α) và (β) là:
A. 2/(√3) B. 2
C. 7/2 D. 7/(2√3)
Bài 3.88: Khoảng cách từ điểm M(2; 0; 1) đến đường thẳng d là:
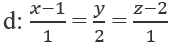
A. √(12) B. √3
C. √2 D. 12/(√6)
Bài 3.89: Bán kính của mặt cầu tâm I(1; 3; 5) và tiếp xúc với đường thẳng là:
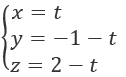
A. √(14) B. 14
C. √7 D. 7
Bài 3.90: Khoảng cách giữa hai đường thẳng:
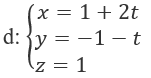
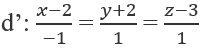
A. √6 B. (√6)/2
C. 1/(√6) D. √2
Bài 3.91: Tọa độ hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng
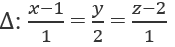
A. (1; 0; 2) B. (2; 2; 3)
C. (0; -2; 1) D. (-1; -4; 0)
Bài 3.92: Cho mặt phẳng (α): 3x - 2y - z + 5 = 0
và đường thẳng
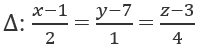
Gọi (β) là mặt phẳng chứa Δ và song song với (α). Khoảng cách giữa (α) và (β) là:
A. 9/14 B. 9/(√(14))
C. 3/14 D. 3/(√(14))
Lời giải:
Đáp án và hướng dẫn giải
| 3.68. B | 3.69. A | 3.70. C | 3.71. A | 3.72. D |
| 3.73. B | 3.74. A | 3.75. A | 3.76. B | 3.77. C |
| 3.78. B | 3.79. A | 3.80. C | 3.81. D | 3.82. C |
| 3.83. A | 3.84. C | 3.85. B | 3.86. B | 3.87. D |
| 3.88. C | 3.89. A | 3.90. B | 3.91. A | 3.92. B |
Bài 3.68: Chọn B.
Mặt phẳng (α) có hai vectơ chỉ phương là
EF→ = (-1; 2; -2) và j→ = (1; 0; 0)
nên vectơ pháp tuyến n→ = [EF→, i→] = (0; -2; -2) = -2(0; 1; 1)
Suy ra phương trình (α) là y + z = 0.
Bài 3.69: Chọn A.
(α) có vectơ pháp tuyến là (1; -4; 1) và đi qua điểm A nên có phương trình là (x - 1) - 4(y - 2) + (z - 3) = 0 hay x - 4y + z + 4 = 0
Bài 3.70: Chọn C.
(γ) vuông góc với Oz, vậy mệnh đề (γ) // Oz sai.
Bài 3.71: Chọn A.
Mặt phẳng chứa trục Oy và điểm Q sẽ có hai vectơ chỉ phương là: OQ→ = (1; 4; -3) và j→ = (0; 1; 0) nên có vectơ pháp tuyến là [OQ→, j→] = (3; 0; 1)
Và mặt phẳng đi qua gốc O nên có phương trình là: 3x + z = 0
Bài 3.72: Chọn D.
Mặt phẳng (α) chứa điểm O và có vectơ (0; 2; 1) vuông góc với i→ = (1; 0; 0) nên (α) ⊃ Ox
Bài 3.73: Chọn B.
Mặt phẳng (α) chứa điểm A và có vectơ pháp tuyến là BC→ = (1; -2; -5) nên có phương trình là:
1(x - 2) - 2(y - 1) - 5(z + 1) = 0 hay x - 2y - 5z - 5 = 0
Bài 3.74: Chọn A.
Mặt phẳng (γ) có hai vectơ chỉ phương là (3; -2; 2) và (5; -4; 3) nên có vectơ pháp tuyến là (2; 1; -2). Phương trình (γ) có dạng là:
2(x - 3) - 2(y - 1) - 5(z + 1) = 0 hay 2x + y - 2z - 15 = 0
Bài 3.75: Chọn A.
Đường thẳng d đi qua điểm M(2; 0; -3) và có vectơ chỉ phương là a→ nên phương trình chính tắc là:
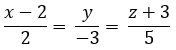
Bài 3.76: Chọn B.
Đường thẳng d đi qua điểm M(2; 1; 0) và có vectơ chỉ phương là a→ = (-1; 1; 1) nên có phương trình chính tắc là:
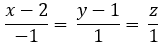
Bài 3.77: Chọn C.
Đường thẳng AB đi qua điểm A(1; 2; -3) và có vectơ chỉ phương là a→ = (-1; 1; 1) nên có phương trình chính tắc là:
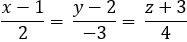
Bài 3.78: Chọn B.
Thay tọa độ điểm M(12 + 4t; 9 + 3t; 1 + t) thuộc d vào phương trình mặt phẳng (α), ta được phương trình theo t:
3(12 + 4t) + 5(9 + 3t) - (1 + t) - 2 = 0. Giải phương trình ta được t = -3.
Vậy d cắt (α) tại M(0; 0; -2).
Bài 3.79: Chọn A.
Đường thẳng d có vectơ chỉ phương là (1; -1; 2) vuông góc với vectơ pháp tuyến (1; 3; 1) của mặt phẳng (α) và điểm cố định M(1; 2; 1) của d không thuộc (α). Vậy d // (α)
Bài 3.80: Chọn C.
Đường thẳng d có vectơ chỉ phương là (1; 2; -3) vuông góc với vectơ pháp tuyến (1; 1; 1) của mặt phẳng (α) và điểm cố định M(1; 1; 2) của d nằm trên (α). Vậy d ⊂ (α)
Bài 3.81: Chọn D.
Hai đường thẳng d và d' có hai vectơ chỉ phương tỉ lệ:
(2; 2; -2) = 2(1; 1; -1) và một điểm của đường này không nằm trên đường kia. Suy ra d // d'.
Bài 3.82: Chọn C.
Giải hệ phương trình:
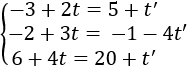
Ta được t = 3; t' = -2. Vậy giao điểm của d và d' là M(3; 7; 18).
Bài 3.83: Chọn A.
Hai đường thẳng d và d' có hai vectơ chỉ phương không tỉ lệ là:
a→ = (m; 1; 2), a'→ = (-1; 2; -1).
Hai điểm M(1; 0; -1) và M'(1; 2; 3) lần lượt thuộc d và d'.
Ta có MM'→ = (0; 2; 4)
d và d' cắt nhau ⇔ [a→.a'→].MM'→ = 0
⇔ 2(m - 2) + 4(2m + 1) = 0
⇔ m = 0
Bài 3.84: Chọn C.
Ta có:
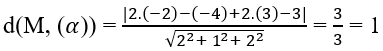
Bài 3.85: Chọn B.
Ta có:
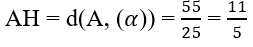
Bài 3.86: Chọn B.
Mặt cầu tâm I bán kính r tiếp xúc với mặt phẳng (P) khi
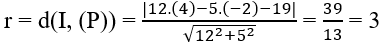
Bài 3.87: Chọn D.
Lấy điểm M(0; 0; 5) thuộc (α). Ta có khoảng cách giữa (α) và (β) bằng khoảng cách từ M đến (β) và bằng 7/(2√3).
Bài 3.88: Chọn C.
Lấy điểm A(1; 0; 2) trên d và một vectơ chỉ phương của d là a→ = (1; 2; 1)
AM→ = (1; 0; -1)
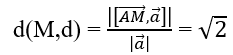
Bài 3.89: Chọn A.
Bán kính của mặt cầu tâm I(1; 3; 5) và tiếp xúc với đường thẳng d bằng khoảng cách từ I đến d bằng √(14).
Bài 3.90: Chọn B.
d đi qua điểm M(1; -1; 1) và có vectơ chỉ phương a→ = (2; -1; 0);
d' đi qua điểm M'(2; -2; 3) và có vectơ chỉ phương a'→ = (-1; 1; 1)
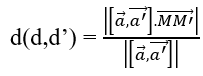
Dùng công thức:
Ta được khoảng cách giữa hai đường thẳng d và d' bằng (√6)/2.
Bài 3.91: Chọn A.
Đường thẳng Δ:
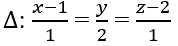
có phương trình tham số là:
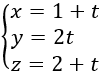
Gọi H(1 + t; 2t; 2 + t) là một điểm trên Δ. Ta có: H là hình chiếu vuông góc của M trên Δ khi: MH→.aΔ→ = 0. Ta tìm được t = 0. Suy ra H(1; 0; 2)
Bài 3.92: Chọn B.
Khoảng cách giữa (α) và (β) bằng khoảng cách từ điểm M(1; 7; 3) trên (β) đến (α). Ta có: