Bài tập trắc nghiệm trang 64, 65, 66 Sách bài tập Hình học 12

---

Câu hỏi trắc nghiệm chương 2

Bài tập trắc nghiệm trang 64, 65, 66 Sách bài tập Hình học 12:

Bài 2.33: Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S₁ là diện tích 6 mặt của hình lập phương, S₂ là diện tích xung quanh của hình trụ. Tỉ số S₂/S₁ bằng:

A. π/6              B. 1/2

C. π/2              D. π

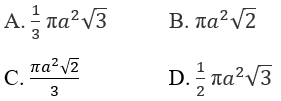
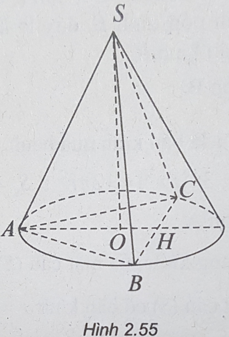
Bài 2.34: Một hình tứ diện đều cạnh a có một đỉnh trùng với đỉnh của hình nón tròn xoay còn ba đỉnh còn lại của tứ diện nằm trên đường tròn đáy của hình nón. Diện tích xung quanh của hình nón tròn xoay là:

Bài 2.35: Khẳng đỉnh nào sau đây là sai?

A. Có một mặt cầu đi qua các đỉnh của một tứ diện bất kì.

B. Có một mặt cầu đi qua các đỉnh của một hình lăng trụ có đáy là một tứ giác lồi.

C. Có một mặt cầu đi qua các đỉnh của một hình hộp chữ nhật.

D. Có một mặt cầu đi qua các đỉnh của một hình chóp đều.

Bài 2.36: Cho ba điểm A, B, C cùng thuộc một mặt cầu và biết rằng ∠ACB = 90^o.

Khẳng định nào sau đây là đúng?

A. AB luôn là đường kính của mặt cầu đã cho.

B. Luôn luôn có một đường tròn thuộc mặt cầu ngoại tiếp tam giác ABC.

C. Tam giác ABC vuông cân tại C.

D. AB là đường kính của một đường tròn lớn trên mặt cầu đã cho.

Bài 2.37: Cho tứ diện ABCD có AD ⊥ (ABC) và BD ⊥ BC. Khi quay tứ diện đó xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?

A. Một              B. Hai

C. Ba              D. Bốn

Bài 2.38: Khẳng định nào sau đây là sai?

Các hình chóp sau đây luôn có các đỉnh nằm trên một mặt cầu:

A. Hình chóp tam giác              B. Hình chóp ngũ giác đều

C. Hình chóp tứ giác              D. Hình chóp đều n-giác.

Bài 2.39: Cho tứ diện đều ABCD. Khi quay tứ diện đó xung quanh trục là AB có bao nhiêu hình nón khác nhau được tạo thành?

A. Một              B. Hai

C. Ba              D. Không có hình nón nào

Bài 2.40: Trong một chiếc hộp hình trụ, người ta bỏ vào đấy ba quả banh tennis, biết rằng đáy của hình trụ bằng hình nón lớn trên quả banh và chiều cao của hình trụ bằng ba lần đường kính quả banh. Gọi S₁ là tổng diện tích của ba quả banh, S₂ là diện tích xung quanh của hình trụ. Tỉ số diện tích S₁/S₂ là:

A. 1              B. 5

C. 2              D. Tỉ số đó là một số khác.

Bài 2.41: Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:

A. π(a² + b² + c²)              B. 2π(a² + b² + c²)

C. 4π(a² + b² + c²)              D. π/2.(a² + b² + c²)

Bài 2.42: Cho mặt cầu S(0;R) và mặt phẳng (α). Gọi d là khoảng cách từ O tới (α). Khi d < R thì mặt phẳng (α) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn có bán kính bằng:

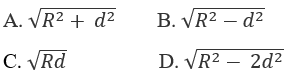
Bài 2.43: Cho tam giác ABC vuông tại A có BC = 2a và ∠B = 30^o. Quay tam giác vuông này quanh trục AB, ta được một hình nón đỉnh B. Gọi S₁ là diện tích toàn phần của hình nón đó và S₂ là diện tích mặt cầu đường kính AB. Khi đó, tỉ số S₁/S₂ là:

A. 1              B. 1/2

C. 2/3              D. 3/2

Bài 2.44: Cho một hình nón với thiết diện qua trục là một tam giác đều cạnh 2a có diện tích xung quanh là S₁ và một mặt cầu có đường kính bằng chiều cao hình nón có diện tích là S₂. Khi đó, hệ thức giữa S₁ và S₂ là:

A. S₁ = S₂              B. S₁ = 4S₂

C. S₂ = 2S₁              D. 2S₂ = 3S₁

Bài 2.45: Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón là:

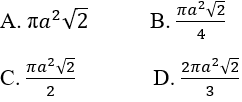
Bài 2.46: Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a√2 và góc giữa đường sinh và mặt phẳng đáy bằng 60^o. Diện tích xung quanh S_xp của hình nón và thể tích V của khối nón tương ứng là:

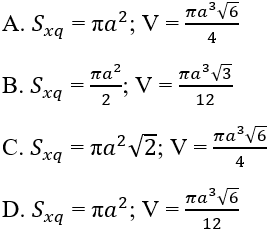
Bài 2.47: Trong không gian, cho tam giác ABC vuông tại A, AB = a và AC = a√3. Khi quay tam giác ABC xung quanh AB, ta được một khối nón có độ dài đường sinh là:

A. l = 2a              B. l = a√2

C. l = a√3              D. l = a

Bài 2.48: Cho hình trụ có bán kính đáy a và có thiết diện qua trục là một hình vuông. Diện tích xung quanh của hình trụ là:

A. 3πa²              B. 2πa²

C. 4πa²              D. πa²

Bài 2.49: Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:

A. 2πa³              B. 2πa³/3

C. 4πa³              D. πa³

Lời giải:

2.33. A	2.34. A	2.35. B	2.36. B	2.37. B	2.38. C
2.39. B	2.40. A	2.41. A	2.42.B	2.43. A	2.44. D
2.45. C	2.46. D	2.47. A	2.48. C	2.49. A

Bài 2.33: Chọn A.

Ta có: S₁ = 6a²; S₂ = πa²

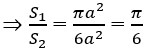
Bài 2.34: Chọn A.

(h.2.55) Ta có:

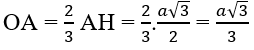
SA = a

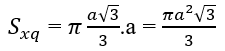
Bài 2.35: Chọn B.

Nếu có một mặt cầu ngoại tiếp lăng trụ thì đáy của lăng trụ phải nội tiếp trong một đường tròn, điều này không đúng cho tứ giác lồi bất kì.

Bài 2.36: Chọn B.

Mặt phẳng (ABC) cắt mặt cầu theo đường tròn ngoại tiếp tam giác ABC.

Bài 2.37: Chọn B.

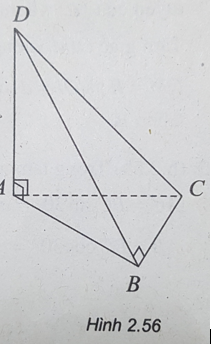
(h.2.56) Khi quay tứ diện quanh AB, AD và BC nằm trên hai mặt phẳng song song với nhau, cùng vuông góc với AB lần lượt tại A và B. Ta có hai hình nón: Hình nón đỉnh A, đường cao AB, bán kính đáy là BC. Hình nón đỉnh B, đường cao BA, bán kính đáy là AD.

Bài 2.38: Chọn C.

Điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.

Bài 2.39: Chọn B.

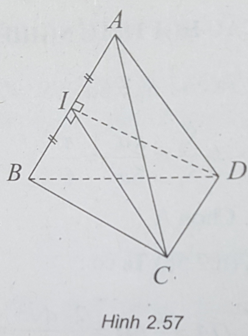
(h.2.57) Gọi I là trung điểm AB. Dễ thấy IC = ID. Khi quay tứ diện quanh AB, ta có hai hình nón: Hình nón đỉnh A, đáy là hình tròn tâm I, bán kính IC; Hình nón đỉnh B, đáy là hình tròn tâm I, bán kính IC.

Bài 2.40: Chọn A.

Gọi r là bán kính quả banh. Ta có:

S₁ = 3(4πr²) = 12πr²;

S₂ = (2πr).6r = 12πr².

Bài 2.41: Chọn A.

Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính

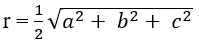
Do đó diện tích mặt cầu (S) là: S = 4πr² = π(a² + b² + c²)

Bài 2.42: Chọn B.

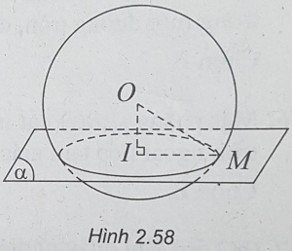
(h.2.58) Gọi I là hình chiếu của O lên (α) và M là điểm thuộc đường giao tuyến của (α) và mặt cầu S(O;R).

Tam giác OIM vuông tại I, ta có:

OM = R và OI = d

nên

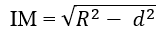
Bài 2.43: Chọn A.

(h.2.59) Trong tam giác ABC vuông tại A, ta có:

AC = BC.sin30^o = a;

AB = BC.cos30^o = a√3.

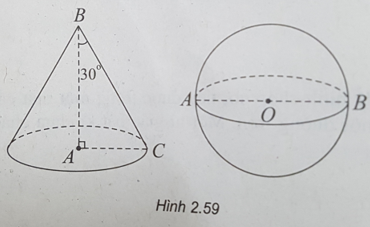
Diện tích toàn phần hình nón là:

S₁ = S_xq + S_đáy = πRl + πR² = πa.2a + πa² = 3πa²

Diện mặt cầu đường kính AB là:

S₂ = πAB² = π(a√3)² = 3πa²

Từ đó suy ra, tỉ số S₁/S₂ = 1

Bài 2.44: Chọn D.

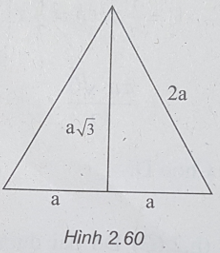
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.

Do đó, ta có:

S₁ = πRl = π.a.2a = 2πa² (1)

Mặt cầu có bán kính là a√3/2, nên ta có:

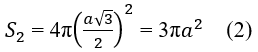
Từ (1) và (2) suy ra: 2S₂ = 3S₁

Bài 2.45: Chọn C.

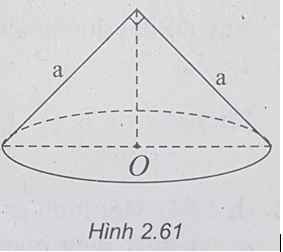
(h.2.61) Thiết diện qua trục là một tam giác vuông cân cạnh a nên đường sinh của hình nón là a và bán kính đáy là (a√2)/2

Suy ra:

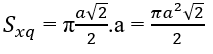
Bài 2.46: Chọn D.

(h.2.62) Gọi A là một điểm thuộc đường tròn đáy của hình nón. Dựa vào giả thiết, ta có đường sinh SA = a√2 và góc giữa đường sinh và mặt phẳng đáy là ∠SAO = 60^o.

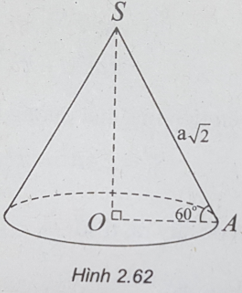
Trong tam giác vuông SAO, ta có:

OA = SA.cos60^o = (a√2)/2;

SO = SA.sin60^o = (a√6)/2.

Diện tích xung quanh hình nón:

S_xq = πrl = πa².

Thể tích của khối nón tròn xoay:

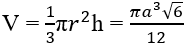
Bài 2.47: Chọn A.

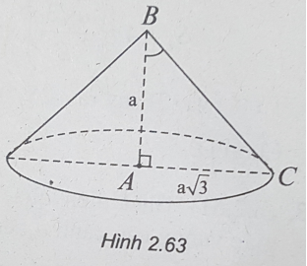
(h.2.63) Độ dài đường sinh l bằng độ dài cạnh BC của tam giác vuông ABC.

Theo định lý Py-ta-go, ta có:

BC² = AB² + AC² = a² + 3a² = 4a²

⇒ BC = 2a.

Vậy độ dài đường sinh của hình nón là l = 2a.

Bài 2.48: Chọn C.

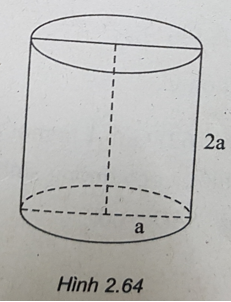
(h.2.63) Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông nên chiều cao hình trụ bằng 2a.

Vậy diện tích xung quanh khối trụ là:

S_xq = 2πRh = 4πa².

Bài 2.49: Chọn A.

Thiết diện qua trục của hình trụ là hình vuông nê hình trụ có bán kính đáy là a, chiều cao là 2a.

Do đó thể tích khối trụ là:

V = πR²h = 2πa³.