(SGK + SBT) Giải Toán 8 trang 93 Kết nối tri thức, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 93 Kết nối tri thức, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 93.
(SGK + SBT) Giải Toán 8 trang 93 Kết nối tri thức, Cánh diều
- Toán lớp 8 trang 93 Tập 1 (sách mới):
- Toán lớp 8 trang 93 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 93 (sách cũ)
Bài 104 trang 93 SBT Toán 8 Tập 1: Cho góc xOy và điểm A nằm trong góc đó.
a. Vẽ điểm B đối xứng với O qua A. Qua B vẽ đường thẳng song song với Ox, cắt Oy ở C. Gọi D là giao điểm của CA và Ox. Chứng minh rằng các điểm C và D đối xứng với nhau qua điểm A.
b. Từ đó suy ra cách dựng hình đường thẳng đi qua A, cắt OX, Oy ở C, D sao cho A là trung điểm của CD.
Lời giải:
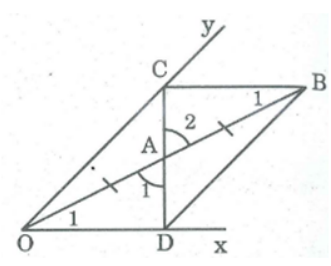
a. Xét ΔOAD và ΔBAC, ta có:
OA = OB (tính chất đối xứng tâm)
∠A1= ∠A2(đối đỉnh)
∠O1= ∠B1(so le trong)
Do đó: ΔOAD = ΔBAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua tâm A.
b. Cách dựng:
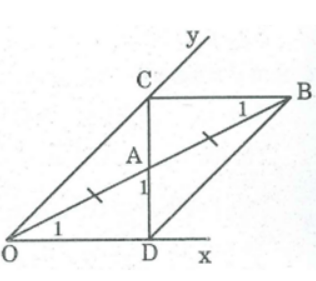
- Dựng B đối xứng với O qua tâm A.
- Qua B dựng đường thẳng song song Ox cắt Oy tại C.
- Dựng tia CA cắt OX tại D.
Ta có D là điểm cần dựng.
Chứng minh:
Xét ΔOAD và ΔBAC, ta có:
OA = OB (tính chất đối xứng tâm)
∠A1= ∠A2(đối đỉnh)
∠O1= ∠B1(so le trong)
Do đó: ΔOAD = ΔBAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua tâm A.
Bài 105 trang 93 SBT Toán 8 Tập 1: Cho tam giác ABC, điểm M nằm trên cạnh BC. Gọi O là trung điểm của AM. Dựng điểm E thuộc cạnh AB, điểm F thuộc cạnh AC sao cho E đối xứng với F qua O
Lời giải:
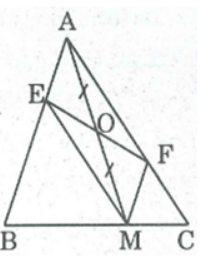
Cách dựng:
- Qua điểm M dựng đường thẳng song song với AC cắt AB tại E.
- Qua điểm M dựng đường thẳng song song với AB cắt AC tại F.
Chứng minh:
Ta có: ME // AC hay ME // AF
MF //AB hay MF // AE
Nên tứ giác AEMF là hình bình hành.
Ta có: O là trung điểm của AM
Suy ra: EF đi qua O (tính chất hình bình hành)
⇒ OE = OF
Vậy E đối xứng với F qua tâm O

