Bài 13, 14, 15, 16, 17, 18 trang 7 SBT Toán 8 tập 2

---

Bài 13, 14, 15, 16, 17, 18 trang 7 SBT Toán 8 tập 2

Bài 13 trang 7 sách bài tập Toán 8 Tập 2: Tìm giá trị của k, biết rắng một trong hai phương trình sau đây nhận x = 5 là nghiệm, phương trình còn lại nhận x = -1 là nghiệm: 2x = 10 và 3 – kx = 2

Lời giải:

Thay x = 5 vào vế trái của phương trình 2x = 10, ta thấy giá trị của hai vế bằng nhau. Vậy x = 5 là nghiệm của phương trình 2x = 10.

Khi đó x = -1 là nghiệm của phương trình 3 – kx = 2.

Thay x = -1 vào phương trình 3 – kx = 2, ta có:

3 – k(-1) = 2 ⇔ 3 + k = 2 ⇔ k = -1

Vậy k = -1.

Bài 14 trang 7 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:

a. 7x + 21 = 0

b. 5x – 2 = 0

c. 12 – 6x = 0

d. -2x + 14 = 0

Lời giải:

a. 7x + 21 = 0 ⇔ 7x = -21 ⇔ x = -3

b. 5x – 2 = 0 ⇔ 5x = 2 ⇔ x = 2/5

c. 12 – 6x = 0 ⇔ 12 = 6x ⇔ x = 2

d. -2x + 14 = 0 ⇔ -2x = -14 ⇔ x = 7

Bài 15 trang 7 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:

a. 0,25x + 1,5 = 0

b. 6,36 – 5,3x = 0

c. 4/3 x - 5/6 = 1/2

d. -5/9 x + 1 = 2/3 x – 10

Lời giải:

a. 0,25x + 1,5 = 0 ⇔ 0,25x = -1,5 ⇔ x = -6

b. 6,36 – 5,3x = 0 ⇔ 6,36 = 5,3x ⇔ x = 1,2

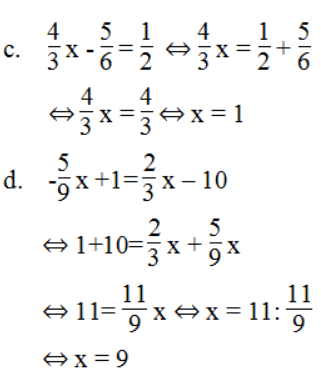
Bài 16 trang 7 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:

a. 3x + 1 = 7x – 11

b. 5 – 3x = 6x + 7

c. 11 – 2x = x – 1

d. 15 – 8x = 9 – 5x

Lời giải:

a. 3x + 1 = 7x – 11 ⇔ 3x – 7x = -11 – 1 ⇔ -4x = -12 ⇔ x = 3

b. 5 – 3x = 6x + 7 ⇔ 5 – 7 = 6x + 3x ⇔ -2 = 9x ⇔ x = -29

c. 11 – 2x = x – 1 ⇔ 11 + 1 = x + 2x ⇔ 12 = 3x ⇔ x = 4

d. 15 – 8x = 9 – 5x ⇔ -8x + 5x = 9 – 15 ⇔ -3x = -6 ⇔ x = 2

Bài 17 trang 7 sách bài tập Toán 8 Tập 2: Chứng tỏ rằng các phương trình sau đây vô nghiệm:

a. 2(x + 1) = 3 + 2x

b. 2(1 – 1,5x) + 3x = 0

c. |x| = -1

Lời giải:

a. Ta có: 2(x + 1) = 3 + 2x ⇔ 2x + 2 = 3 + 2x ⇔ 0x = 1

Vậy phương trình vô nghiệm.

b. Ta có: 2(1 – 1,5x) + 3x = 0 ⇔ 2 – 3x + 3x = 0 ⇔ 2 + 0x = 0

Vậy phương trình vô nghiệm.

c. Vì |x| ≥ 0 nên phương trình |x| = -1 vô nghiệm.

Bài 18 trang 7 sách bài tập Toán 8 Tập 2: Cho phương trình (m² – 4)x + 2 = m. Giải phương trình trong mỗi trường hợp sau:

a. m = 2

b. m = -2

c. m = -2,2

Lời giải:

a. Khi m = 2, phương trình đã cho trở thành:

(2² – 4)x + 2 ⇔ 0x + 2 = 2 ⇔ 2 = 2

Vậy phương trình đã cho có vô số nghiệm.

b. Khi m = -2, phương trình đã cho trở thành:

[(-2)² – 4]x + 2 = -2 ⇔ 0x + 2 = -2 ⇔ 0x = -4

Vậy phương trình đã cho vô nghiệm.

c. Khi m = -2,2, phương trình đã cho trở thành:

[(-2,2)² – 4]x + 2 = -2,2 ⇔ 0,84x + 2 = -2,2

⇔ 0,84x = -2,2 – 2 ⇔ 0,84x = -4,2 ⇔ x = -5

Vậy phương trình đã cho có nghiệm x = -5.