(SGK + SBT) Toán 8 Bài 20 (sách mới) | Kết nối tri thức

---

Haylamdo giới thiệu lời giải bài tập Toán 8 Bài 20 đầy đủ sgk, sbt Kết nối tri thức sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài 20.

(SGK + SBT) Toán 8 Bài 20 (sách mới) | Kết nối tri thức

- Giải sgk Toán 8 Bài 20 (sách mới):

• (Kết nối tri thức) Giải Toán 8 Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ

  Xem lời giải

- Giải sbt Toán 8 Bài 20 (sách mới):

• (Kết nối tri thức) Giải SBT Toán 8 Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ

  Xem lời giải

---

---

---

Lưu trữ: Giải SBT Toán 8 Bài 20 trang 8 sách bài tập Toán 8 Tập 2 (sách cũ)

Bài 20 trang 8 sách bài tập Toán 8 Tập 2: Giải các phương trình sau

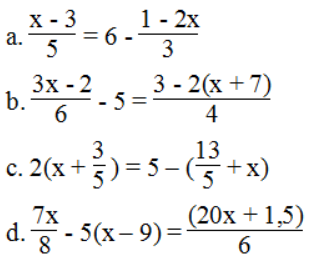
Lời giải:

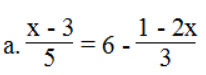
⇔ 3(x – 3) = 6.15 – 5(1 – 2x)

⇔ 3x – 9 = 90 – 5 + 10x

⇔ 3x – 10x = 90 – 5 + 9

⇔ -7x = 94 ⇔ x = - 94/7

Phương trình có nghiệm x = - 94/7

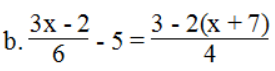
⇔ 2(3x – 2) – 5.12 = 3[3 – 2(x + 7)]

⇔ 6x – 4 – 60 = 9 – 6(x + 7)

⇔ 6x – 64 = 9 – 6x – 42

⇔ 6x + 6x = 9 – 42 + 64

⇔ 12x = 31 ⇔ x = 31/12

Phương trình có nghiệm x = 31/12

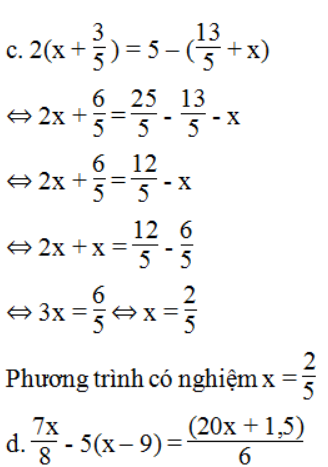
⇔ 3.7x – 24.5(x – 9) = 4(20x + 1,5)

⇔ 21x – 120(x – 9) = 80x + 6

⇔ 21x – 120x + 1080 = 80x + 6

⇔ 21x – 120x – 80x = 6 – 1080

⇔ -179x = -1074 ⇔ x = 6

Phương trình có nghiệm x = 6.

Bài 21 trang 8 sách bài tập Toán 8 Tập 2: Tìm điều kiện của x để giá trị mỗi phân thức sau xác định:

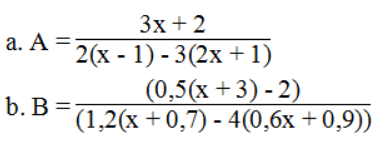
Lời giải:

a. Phân thức 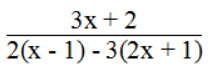xác định khi:

2(x – 1) – 3(2x + 1) ≠ 0

Ta giải phương trình: 2(x – 1) – 3(2x + 1) = 0

Ta có: 2(x – 1) – 3(2x + 1) = 0 ⇔ 2x – 2 – 6x – 3 = 0

⇔ -4x – 5 = 0 ⇔ 4x = -5 ⇔ x = -54

Vậy khi x ≠ -54 thì phân thức A xác định.

b. Phân thức 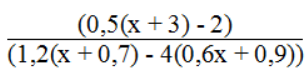xác định khi:

1,2(x + 0,7) – 4(0,6x + 0,9) ≠ 0

Ta giải phương trình: 1,2(x + 0,7) – 4(0,6x + 0,9) = 0

Ta có: 1,2(x + 0,7) – 4(0,6x + 0,9) = 0

⇔ 1,2x + 0,84 – 2,4 – 3,6 = 0

⇔ -1,2x – 2,76 = 0 ⇔ x = -2,3

Vậy khi x ≠ -2,3 thì phân thức B xác định.

Bài 22 trang 8 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:

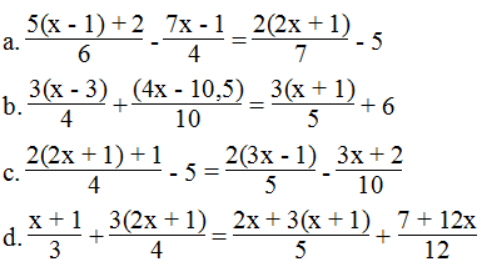
Lời giải:

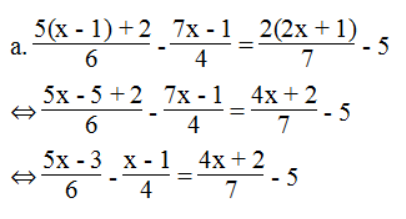
⇔ 14(5x – 3) – 21(7x – 1) = 12(4x + 2) – 5.84

⇔ 70x – 42 – 147x + 21 = 48x + 24 – 420

⇔ 70x – 147x – 48x = 24 – 420 + 42 – 21

⇔ -125x = -375 ⇔ x = 3

Phương trình có nghiệm x = 3

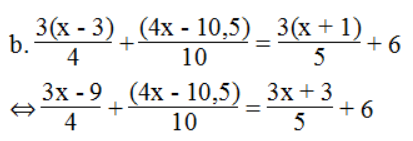
⇔ 5(3x – 9) + 2(4x – 10,5) = 4(3x + 3) + 6.20

⇔ 15x – 45 + 8x – 21 = 12x + 12 + 120

⇔ 15x + 8x – 12x = 12 + 120 + 45 + 21 ⇔ 11x = 198 ⇔ x = 18

Phương trình có nghiệm x = 18

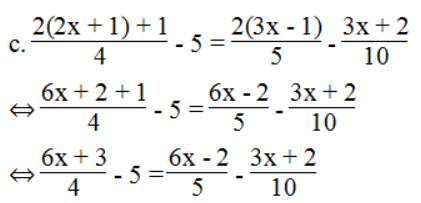
⇔ 5(6x + 3) – 5.20 = 4(6x – 2) – 2(3x + 2)

⇔ 30x + 15 – 100 = 24x – 8 – 6x – 4

⇔ 30x – 24x + 6x = -8 -4 – 15 + 100

⇔ 12x = 73 ⇔ x = 73/12

Phương trình có nghiệm x = 73/12

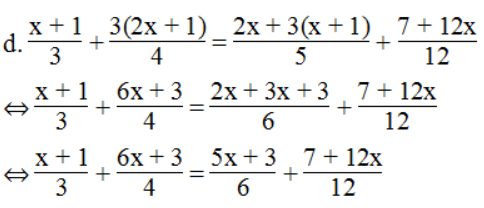
⇔ 4(x + 1) + 3(6x + 3) = 2(5x + 3) + 7 + 12x

⇔ 4x + 4 + 18x + 9 = 10x + 6 + 7 + 12x

⇔ 4x + 18x – 10x – 12x = 6 + 7 – 4 – 9 ⇔ 0x = 0

Phương trình có vô số nghiệm.

Bài 23 trang 8 sách bài tập Toán 8 Tập 2: Tìm giá trị của k sao cho:

a. Phương trình (2x + 1)(9x + 2k) – 5(x + 2) = 40 có nghiệm x = 2.

b. Phương trình 2(2x + 1) + 18 = 3(x + 2)(2x + k) có nghiệm x = 1.

Lời giải:

a. Thay x = 2 vào phương trình (2x + 1)(9x + 2k) – 5(x + 2) = 40, ta có:

(2.2 + 1)(9.2 + 2k) – 5(2 + 2) = 40

⇔ (4 + 1)(18 + 2k) – 5.4 = 40 ⇔ 5(18 + 2k) – 20 = 40

⇔ 90 + 10k – 20 = 40 ⇔ 10k = 40 – 90 + 20 ⇔ 10k = -30

⇔ k = -3

Vậy khi k = -3 thì phương trình (2x + 1)(9x + 2k) – 5(x + 2) = 40 có nghiệm x = 2.

b. Thay x = 1 vào phương trình 2(2x + 1) + 18 = 3(x + 2)(2x + k), ta có:

2(2.1 + 1) + 18 = 3(1 + 2)(2.1 + k)

⇔ 2(2 + 1) + 18 = 3.3(2 + k) ⇔ 2.3 + 18 = 9(2 + k)

⇔ 6 + 18 = 18 + 9k ⇔ 24 – 18 = 9k ⇔ 6 = 9k ⇔ k = 69 = 23

Vậy khi k = 23 thì phương trình 2(2x + 1) + 18 = 3(x + 2)(2x + k) có nghiệm x = 1.

Bài 24 trang 8 sách bài tập Toán 8 Tập 2: Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau:

a. A = (x – 3)(x + 4) – 2(3x – 2); B = (x – 4)²

b. A = (x + 2)(x – 2) + 3x²; B = (2x + 1)² + 2x

c. A = (x – 1)(x² + x + 1) – 2x; B = x(x – 1)(x + 1)

d. A = (x + 1)³ – (x – 2)³; B = (3x – 1)(3x + 1)

Lời giải:

a. Ta có: A = B ⇔ (x – 3)(x + 4) – 2(3x – 2) = (x – 4)²

⇔ x² + 4x – 3x – 12 – 6x + 4 = x² – 8x + 16

⇔ x² – x² + 4x – 3x – 6x + 8x = 16 + 12 – 4

⇔ 3x = 24 ⇔ x = 8

Vậy với x = 8 thì A = B

b. Ta có: A = B ⇔ (x + 2)(x – 2) + 3x² = (2x + 1)² + 2x

⇔ x² – 4 + 3x² = 4x² + 4x + 1 + 2x

⇔ x² + 3x² – 4x² – 4x – 2x = 1 + 4 ⇔ -6x = 5 ⇔ x = - 5/6

Vậy với x = - 5/6 thì A = B.

c. Ta có: A = B ⇔ (x – 1)(x² + x + 1) – 2x = x(x – 1)(x + 1)

⇔ x³ – 1 – 2x = x(x² – 1) ⇔ x³ – 1 – 2x = x³ – x

⇔ x³ – x³ – 2x + x = 1 ⇔ -x = 1 ⇔ x = -1

Vậy với x = -1 thì A = B

d. Ta có: A = B ⇔ (x + 1)³ – (x – 2)³ = (3x – 1)(3x + 1)

⇔ x³ + 3x² + 3x + 1 – x³ + 6x² – 12x + 8 = 9x² – 1

⇔ x³ – x³ + 3x² + 6x² – 9x² + 3x – 12x = -1 – 1 – 8

⇔ -9x = -10 ⇔ x = 10/9

Vậy với x = 10/9 thì A = B.