Bài 37, 38, 39, 40, 41 trang 162 SBT Toán 8 tập 1

---

Bài 37, 38, 39, 40, 41 trang 162 SBT Toán 8 tập 1

Bài 37 trang 162 SBT Toán 8 Tập 1: Chứng minh rằng mọi đường thẳng đi qua trung điểm của đường trung bình của hình thang và cắt hai dây hình thang sẽ chia hình thang đó thành hai hình thang có diện tích bằng nhau.

Lời giải:

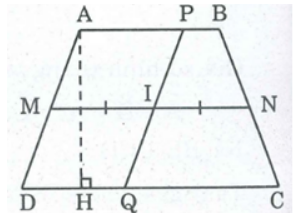
Giả sử hình thang ABCD có AB // CD, đường trung bình là MN. Gọi I là trung điểm của MN, đường thẳng bất kỳ đi qua I cắt AB tại P và CD tại Q.

Ta có hai hình thang APQD và BPQC có cùng đường cao.

MI là đường trung bình của hình thang APQD.

Suy ra: MI = 1/2 (AP + QD)

IN là đường trung bình của hình thang BPQC.

Suy ra: IN = 1/2 (BP + QC)

SAPQD = 1/2 (AP + QD).AH = MI.AH (1)

SBPQC = 1/2 (BP + QC).AH = IN.AH (2).

IM = IN (gt) (3)

Từ (1), (2) và (3) suy ra: S_APQD = S_BPQC, các giá trị này không phụ thuộc vào vị trí của P và Q.

Bài 38 trang 162 SBT Toán 8 Tập 1: Diện tích hình bình hành bằng 24cm². Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng 2cm và 3cm. Tính chu vi của hình bình hành.

Lời giải:

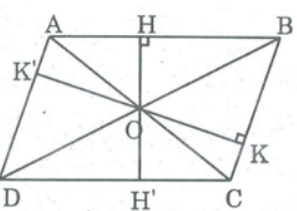
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm

* Kéo dài OH cắt cạnh CD tại H'.

Ta có OH ⊥ BC

⇒ OH' ⊥ CD và OH' = 2cm

Suy ra HH' bằng đường cao của hình bình hành.

S_ABCD = HH'.AB

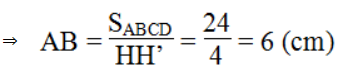
* Kéo dài OK cắt AD tại K'.

Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)

Suy ra KK' là đường cao của hình bình hành.

S_ABCD = KK'.AB

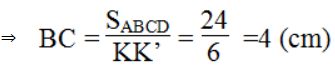
Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).

Bài 39 trang 162 SBT Toán 8 Tập 1: Một hình chữ nhật có các kích thước a và b. Một hình bình hành cũng có hai cạnh là a và b. Tính góc nhọn của hình bình hành nếu diện tích của nó bằng một nửa diện tích hình chữ nhật (a và b có cùng đơn vị đo).

Lời giải:

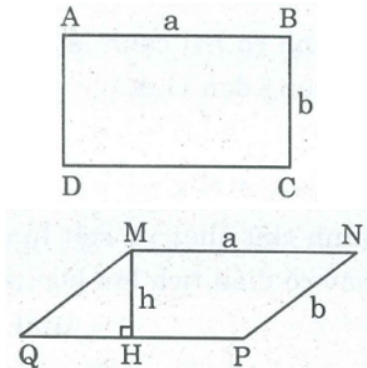
* Xét hình chữ nhật ABCD có chiều dài AB = a, chiều rộng AD = b.

Ta có: S_ABCD = ab.

* Hình bình hành MNPQ có góc M là góc tù, MN = a, cạnh MQ = b

Kẻ đường cao MH. Ta có: S_MNPQ = MH.a

Theo bài ra, ta có: MH.a = 1/2 ab

Suy ra: MH = 1/2 b hay MH = MQ/2

Tam giác MHQ vuông tại H và MH = MQ/2

Cạnh đối diện góc nhọn bằng một nửa cạnh huyền nên ∠(MQH) = 30^o

Vậy góc nhọn của hình bình hành bằng 30^o.

Bài 40 trang 162 SBT Toán 8 Tập 1: Hai cạnh của một hình hình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp số.

Lời giải:

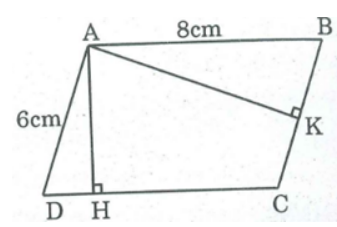
Giả sử hình bình hành ABCD cói AB = 8cm, AD = 6cm.

a. Kẻ AH ⊥ CD, AK ⊥ BC.Ta có 5 < 6, 5 < 8

Đường cao là cạnh góc vuông nhỏ hơn cạnh huyền thỏa mãn có hai trường hợp:

*Trường hợp 1: AK = 5cm

Ta có: S_ABCD = AK.BC = 5.6 = 30 (cm²)

S_ABCD = AH.AD = 8.AH

Suy ra: 8.AH = 30 ⇒ AH = 30/8 = 15/4 (cm)

*Trường hợp 2: AH = 5cm

Ta có: S_ABCD = AH.CD= 5.8 = 40 (cm²)

S_ABCD = AK.BC = 6.AH

Suy ra: 6.AK = 40 ⇒ AK = 40/6 = 20/3 (cm)

Vậy đường cao thứ hai có độ dài là 15/4 cm hoặc 20/3 cm

Bài toán có hai đáp số.

Bài 41 trang 162 SBT Toán 8 Tập 1: Một hình chữ nhật và một hình bình hành có hai cạnh là a và b. Hỏi hình nào có diện tích lớn hơn (a vàb có cùng đơn vị đo).

Lời giải:

Hình chữ nhật có hai cạnh là a và b nên S_{chữ nhật} = ab

Hình bình hành có hai cạnh là a và b. Kẻ đường cao ứng với cạnh bằng ạ thì h < b (vì cạnh góc vuông nhỏ hơn cạnh huyền).

Nếu kẻ đường cao ứng với cạnh bằng b thì h < a (cạnh góc vuông nhỏ hơn cạnh huyền).

Diện tích của hình bình hành là: S_{hình bình hành} = a.h = b.h'

Mà h < b và h' < a nên S_{bình hành} < S_{chữ nhật}