Bài 38, 39, 40 trang 12 SBT Toán 8 tập 2

---

Bài 38, 39, 40 trang 12 SBT Toán 8 tập 2

Bài 38 trang 12 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:

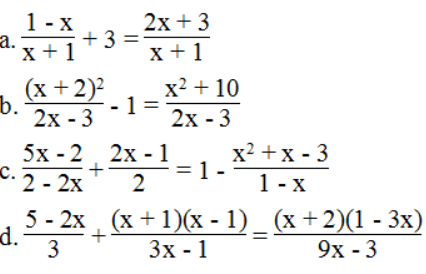
Lời giải:

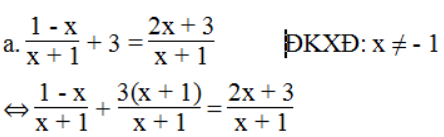
⇔ 1 – x + 3(x + 1) = 2x + 3

⇔ 1 – x + 3x + 3 – 2x – 3 = 0

⇔ 0x = - 1

Phương trình vô nghiệm.

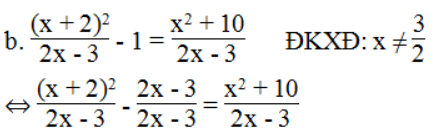
⇔ (x + 2)2 – (2x – 3) = x² + 10

x² + 4x + 4 – 2x + 3 – x² – 10 = 0

⇔ 2x = 3 ⇔ x = 3/2 (loại)

Phương trình vô nghiệm.

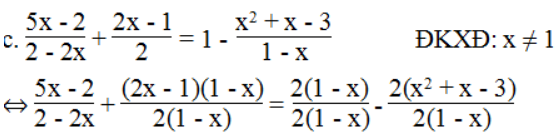
⇔ 5x – 2 + (2x – 1)(1 – x) = 2(1 – x) – 2(x² + x – 3)

⇔ 5x – 2 + 2x – 2x² – 1 + x – 2 + 2x + 2x² + 2x – 6 = 0

⇔ 5x + 2x + x + 2x + 2x = 2 + 6 + 2 + 1 ⇔ 12x = 11

⇔ x = 11/12 (thoả)

Vậy phương trình có nghiệm x = 11/12

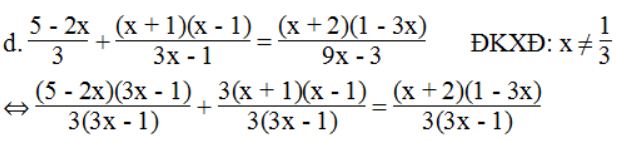
⇔ (5 – 2x)(3x – 1) + 3(x + 1)(x – 1) = (x + 2)(1 – 3x)

⇔ 15x – 5 – 6x² + 2x + 3x² – 3 = x – 3x² + 2 – 6x

⇔ - 6x² + 3x² + 3x² + 15x + 2x – x + 6x = 2 + 5 + 3

⇔ 22x = 10 ⇔ x = 5/11 (thỏa)

Vậy phương trình có nghiệm x = 5/11 .

Bài 39 trang 12 sách bài tập Toán 8 Tập 2: a. Tìm x sao cho biểu thức 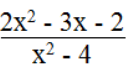bằng 2.

b. Tìm x sao cho giá trị của hai biểu thức sau bằng nhau:

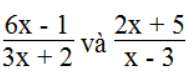
c. Tìm x sao cho giá trị của hai biểu thức sau bằng nhau:

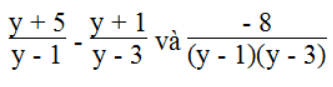
Lời giải:

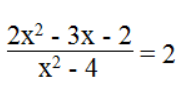
⇔ 2x² - 3x – 2 = 2(x² – 4) ⇔ 2x² – 3x – 2 = 2x² – 8

⇔ 2x² – 2x² – 3x = - 8 + 2 ⇔ - 3x = - 6 ⇔ x = 2 (loại)

Vậy không có giá trị nào của x thỏa mãn điều kiện bài toán.

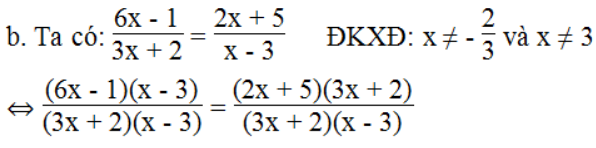
⇔ (6x – 1)(x – 3) = (2x + 5)(3x + 2)

⇔ 6x² – 18x – x + 3 = 6x² + 4x + 15x + 10

⇔ 6x² – 6x² – 18x – x – 4x – 15x = 10 – 3

⇔ - 38x = 7 ⇔ x = - 7/38 (thỏa)

Vậy khi x = - 7/38 thì giá trị của hai biểu thức bằng nhau.

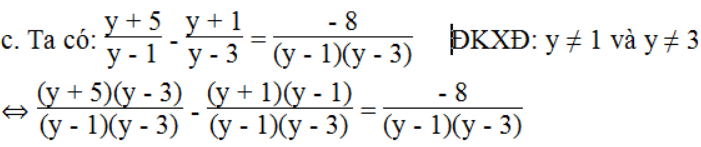
⇔ (y + 5)(y – 3) – (y + 1)(y – 1) = - 8

⇔ y² – 3y + 5y – 15 – y² + 1 = - 8

⇔ 2y = 6 ⇔ y = 3 (loại)

Vậy không có giá trị nào của y thỏa mãn điều kiện bài toán.

Bài 40 trang 12 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:

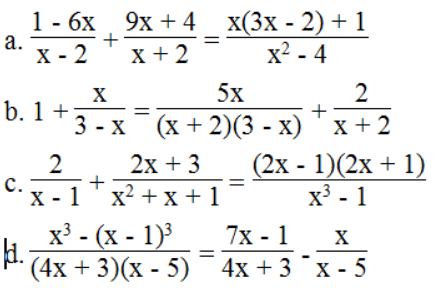
Lời giải:

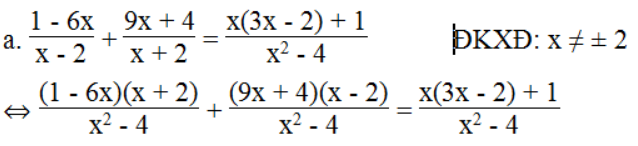
⇔ (1 – 6x)(x + 2) + (9x + 4)(x – 2) = x(3x – 2) + 1

⇔ x + 2 – 6x² – 12x + 9x² – 18x + 4x – 8 = 3x² – 2x + 1

⇔ - 6x² + 9x² – 3x² + x – 12x – 18x + 4x + 2x = 1 – 2 + 8

⇔ - 23x = 7 ⇔ x = - 7/23 (thỏa)

Vậy phương trình có nghiệm x = - 7/23

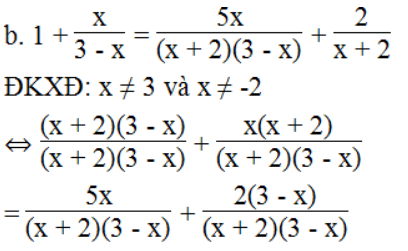
⇔ (x + 2)(3 – x) + x(x + 2) = 5x + 2(3 – x)

⇔ 3x – x² + 6 – 2x + x² + 2x = 5x + 6 – 2x

⇔ x² – x² + 3x – 2x + 2x – 5x + 2x = 6 – 6 ⇔ 0x = 0

Phương trình đã cho có nghiệm đúng với mọi giá trị của x thỏa mãn điều kiện xác định.

Vậy phương trình có nghiệm x ∈ R / x ≠ 3 và x ≠ -2

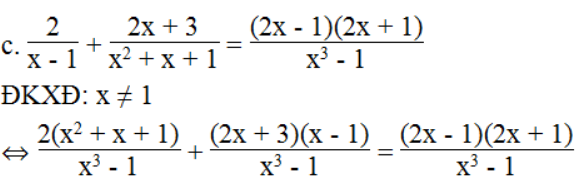
⇔ 2(x² + x + 1) + (2x + 3)(x – 1) = (2x – 1)(2x + 1)

⇔ 2x² + 2x + 2 + 2x² – 2x + 3x – 3 = 4x² – 1

⇔ 2x² + 2x² – 4x² + 2x – 2x + 3x = -1 – 2 + 3

⇔ 3x = 0 ⇔ x = 0 (thỏa)

Vậy phương trình có nghiệm x = 0.

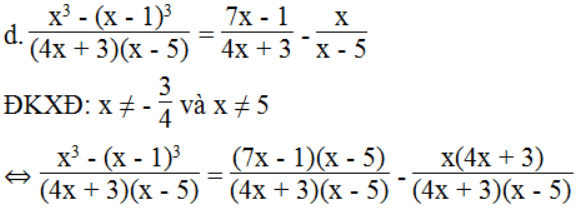
⇔ x³ – (x – 1)3 = (7x – 1)(x – 5) – x(4x + 3)

⇔ x³ – x³ + 3x² – 3x + 1 = 7x² – 35x – x + 5 – 4x² – 3x

⇔ 3x² – 7x² + 4x² – 3x + 35x + x + 3x = 5 – 1

⇔ 36x = 4 ⇔ x = 1/9 (thoả)

Vậy phương trình có nghiệm x = 1/9