Bài 43, 44 trang 85 SBT Toán 8 tập 1

---

Bài 43, 44 trang 85 SBT Toán 8 tập 1

Bài 43 trang 85 SBT Toán 8 Tập 1: Hình thang ABCD có AB // CD; AB = a, BC = b, CD = c, DA = d. Các đường phân giác của góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N.

a. Chứng minh rằng MN // CD

b. Tính độ dài MN theo a, b, c, d (a. b, c, d có cùng đơn vị đo)

Lời giải:

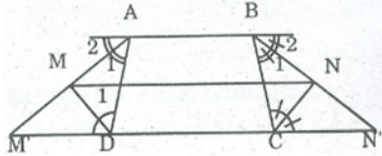
a. Gọi M' và N' là giao điểm của tia AM và BN với CD.

Ta có: ∠(M') = ∠A₂(sole trong)

∠A₁= ∠A₂(gt)

⇒ ∠(M') = ∠A₁nên ΔADM' cân tại D

* DM là phân giác của ∠(ADM' )

Suy ra: DM là đường trung tuyến (tính chất tam giác cân)

⇒ AM = MM'

∠(N') = ∠B₁nên ΔBCN' cân tại C.

* CN là phân giác của ∠(BCN')

Suy ra: CN là đường trung tuyến (tính chất tam giác cân)

⇒ PN = NN'

Suy ra: MN là đường trung bình của hình thang ABN'M'

⇒ MN = M'N' (tính chất đường trung hình hình thang)

Hay MN//CD

b. MN = (AB + MN') / 2 (tỉnh chất đường trung hình hình thang)

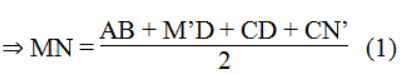
Mà M'D = AD, CN' = BC.

Thay vào (1)

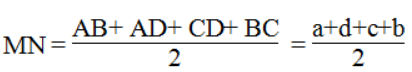
Bài 44 trang 85 SBT Toán 8 Tập 1: Cho tam giác ABC, đường trung tuyến AM. Gọi 0 là trung điểm của AM. Qua O kẻ đường thẳng d cắt các cạnh AB, AC. Gọi AA', BB', CC' là các đường vuông góc kể từ A, B, C đến đường thẳng d.

Chứng minh rằng: AA' = (BB' + CC') / 2

Lời giải:

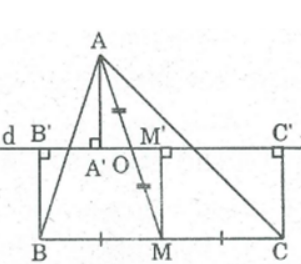
Ta có: BB' ⊥ d (gt)

CC ⊥ d (gt)

Suy ra: BB'// CC'

Tứ giác BB'C'C là hình thang

Kẻ MM' ⊥ d ⇒ MM' // BB' // CC'

Nên MM' là đường trung bình của hình thang BB'C'C

⇒ MM' = (BB' + CC') / 2 (1)

* Xét hai tam giác vuông AA'O và MM'O:

(AA'O) =(MM' O) = 90^o

AO=MO (gt)

(AOA') =(MOM' ) (đối đỉnh)

Do đó: ΔAA'O = ΔMM'O (cạnh huyền, cạnh góc nhọn)

⇒AA' = MM' (2)

Từ (1) và (2) suy ra: AA' = (BB' + CC') / 2