Bài 2.2, 2.3 trang 160 SBT Toán 9 Tập 1

Bài 2.2, 2.3 trang 160 SBT Toán 9 Tập 1

Bài 2 trang 160 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O; 2cm). Vẽ hai dây AB và CD vuông góc với nhau. Tính diện tích lớn nhất của tứ giác ABCD.

Lời giải:

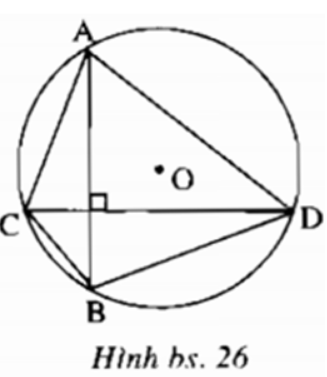
Ta có AB ≤ 4cm, CD ≤ 4cm. Do AB ⊥ CD nên S_ACBD = 1/2AB.CD ≤ 1/2.4.4 = 8 (cm²)

Giá trị lớn nhất của S_ACBD bằng 8 cm² khi AB và CD đều là đường kính của đường tròn.

Bài 3 trang 160 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O;R), dây AB khác đường kính. Vẽ về hai phía của AB các dây AC, AD. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ B đến AC và AD. Chứng minh rằng:

a) Bốn điểm A, H, B, K thuộc cùng một đường tròn;

b) HK < 2R.

Lời giải:

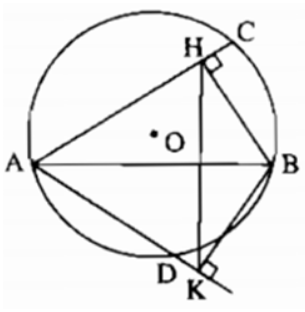
a) Bốn điểm A, H, B, K cùng thuộc đường tròn đường kính AB.

b) Ta có HK ≤ AB ≤ 2R.