Bài 31, 32, 33, 34, 35 trang 10 SBT Toán 9 Tập 1

---

Bài 31, 32, 33, 34, 35 trang 10 SBT Toán 9 Tập 1

Bài 31 trang 10 Sách bài tập Toán 9 Tập 1: Biểu diễn √(ab) ở dạng tích các căn bậc hai với a < 0 và b < 0.

Lời giải:

Vì a < 0 nên -a > 0 và b < 0 nên -b > 0

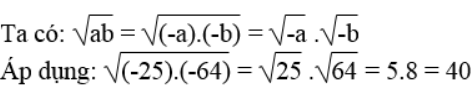
Bài 32 trang 10 Sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức:

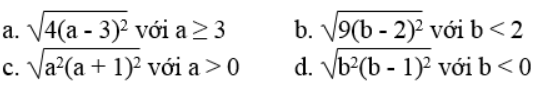
Lời giải:

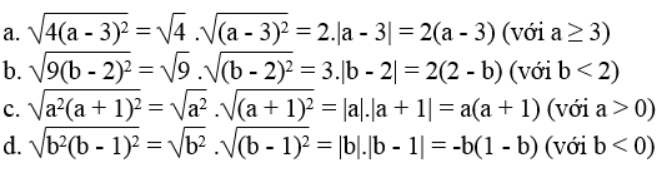
Bài 33 trang 10 Sách bài tập Toán 9 Tập 1: Tìm điều kiện của x để các biểu thức sau có nghĩa và biến đổi chúng về dạng tích:

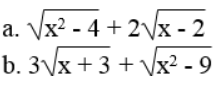
Lời giải:

Bài 34 trang 10 Sách bài tập Toán 9 Tập 1: Tìm x, biết:

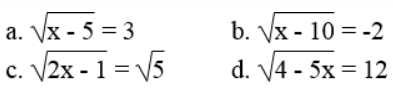
Lời giải:

Bài 35 trang 10 Sách bài tập Toán 9 Tập 1: Với n là số tự nhiên, chứng minh:

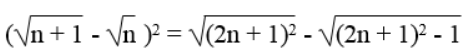
Viết đẳng thức trên khi n bằng 1, 2, 3, 4

Lời giải:

Ta có :

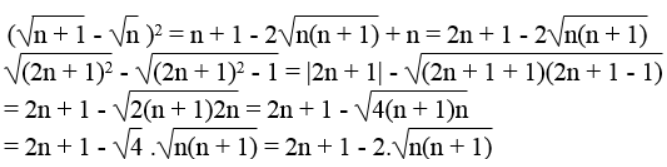
Vế trái bằng vế phải nên đẳng thức được chứng minh.

* Với n = 1, ta có: (√2 - √1 )² = √9 - √8

* Với n = 2, ta có: (√3 - √2 )² = √25 - √24

* Với n = 3, ta có: (√4 - √3 )² = √49 - √48

* Với n = 4, ta có: (√5 - √4 )² = √81 - √80