Bài 37, 38 trang 71 SBT Toán 9 Tập 1

---

Bài 37, 38 trang 71 SBT Toán 9 Tập 1

Bài 37 trang 71 Sách bài tập Toán 9 Tập 1:

a) Cho các điểm M(-1; -2), N(-2; -4), P(2; -3), Q(3; -4,5). Tìm tọa độ của các điểm M’, N’, P’, Q’ lần lượt đối xứng với các điểm M, N, P, Q qua trục Ox.

b) Vẽ đồ thị của các hàm số sau trên cùng một hệ trục tọa độ:

y = |x|;

y = |x + 1|.

c) Tìm tọa độ giao điểm của đồ thị của các hàm số y = |x| và y = |x + 1|.

Từ đó, suy ra phương trình |x| = |x + 1| có nghiệm duy nhất.

Lời giải:

a) (h.25)

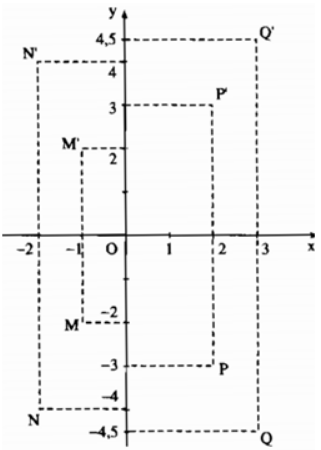
Gọi M’, N’, P’, Q’ là các điểm lần lượt đối xứng qua các điểm M, N, P, Q qua trục Ox, ta thấy rằng hoành độ của các điểm đối xứng nhau qua trục hoành bằng nhau, còn tung độ của các điểm đó thì đối nhau: M’(-1; 2); N’(-2; 4); P’(2; 3); Q’(3; 4,5).

b) (h.26)

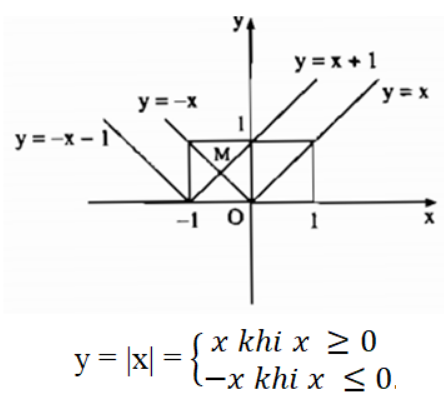
Ta vẽ đồ thị y = x với x ≥ 0.

Vẽ đồ thị y = -x với x ≤ 0.

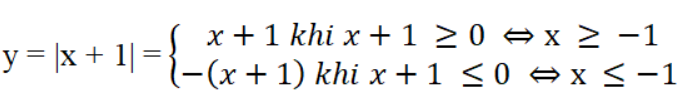
Ta vẽ đồ thị y = x + 1 với x ≥ -1

Vẽ đồ thị y = -x – 1 với x ≤ -1.

c) (h.26) Đồ thị y = -x cắt đồ thị y = x + 1 tại điểm M(x_o, y_o). Vì M thuộc cả hai đồ thị nên tọa độ của M phải thỏa mãn các hàm số, nghĩa là:

y

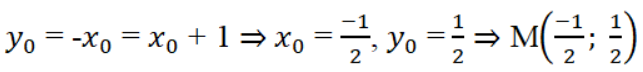
Đồ thị y = |x| và đồ thị y = |x + 1| chỉ cắt nhau tại một điểm duy nhất M((-1)/2; 1/2).

Suy ra phương trình |x| = |x + 1| chỉ có nghiệm duy nhất x = (-1)/2.

Bài 38 trang 71 Sách bài tập Toán 9 Tập 1: Cho các hàm số:

y = 2x – 2 (d₁)

y = - (4/3).x – 2 (d₂)

y = (1/3).x + 3 (d₃)

a. Vẽ đồ thị các hàm số đã cho trên cùng một mặt phẳng tọa độ.

b. Gọi giao điểm của đường thẳng (d₃) với (d₁) và (d₂) theo thứ tự là A và B. Tìm tọa độ của A, B.

c. Tính khoảng cách AB.

Lời giải:

a. *Vẽ đồ thị hàm số y = 2x – 2 (d₁)

Cho x = 0 thì y = -2. Ta có: (0; -2)

Cho y = 0 thì 2x – 2 = 0 ⇔ 2x = 2 ⇔ x = 1. Ta có: (1; 0)

Đồ thị hàm số đi qua hai điểm (0; -2) và (1; 0)

*Vẽ đồ thị hàm số y = - (4/3).x – 2 (d₂)

Cho x = 0 thì y = -2. Ta có: (0; -2)

Cho y = 0 thì - (4/3).x – 2 = 0 ⇔ x = -1,5. Ta có: (-1,5; 0)

Đồ thị hàm số đi qua hai điểm (0; -2) và (-1,5; 0)

*Vẽ đồ thị hàm số y = (1/3).x + 3 (d₃)

Cho x = 0 thì y = 3. Ta có: (0; 3)

Cho y = 0 thì (1/3).x + 3 = 0 ⇔ x = -9. Ta có: (-9; 0)

Đồ thị hàm số đi qua hai điểm (0; 3) và (-9; 0)

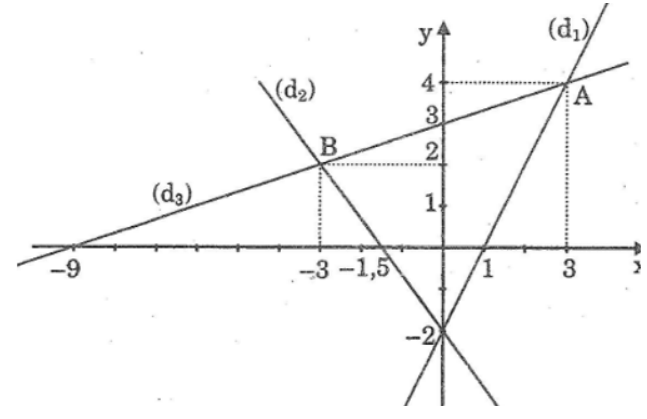
b. Phương trình hoành độ giao điểm của (d₁) và (d₃):

2x – 2 = (1/3).x + 3 ⇔ 2x - (1/3).x = 3 + 2 ⇔ (5/3).x = 5 ⇔ x = 3

Tung độ giao điểm: y = 2.3 – 2 ⇔ y = 6 – 2 = 4

Vậy tọa độ điểm A là A(3; 4)

Phương trình hoành độ giao điểm của (d₂) và (d₃):

- (4/3).x – 2 = (1/3).x + 3 ⇔ (1/3).x + (4/3).x = -2 – 3 ⇔ (5/3).x = -5 ⇔ x = -3

Tung độ giao điểm: y = (1/3).(-3) + 3 ⇔ y = -1 + 3 = 2

Vậy tọa độ điểm B là B(-3; 2)

c. Ta có: AB² = (x_A – x_B)² + (y_A – y_B)² = (3 + 3)² + (4 – 2)² = 40

AB = √40 = 2√10 .