Chứng minh rằng các phép tịnh tiến, đối xứng trục, đối xứng tâm là những phép dời hình

Bài 2: Phép đối xứng qua mặt phẳng và sự bằng nhau của các khối đa diện

Haylamdo biên soạn và sưu tầm lời giải Bài 9 trang 15 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 9 (trang 15 sgk Hình Học 12 nâng cao): Chứng minh rằng các phép tịnh tiến, đối xứng trục, đối xứng tâm là những phép dời hình.

Lời giải:

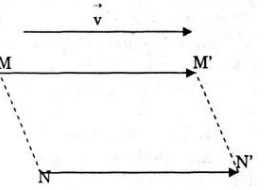
• Phép tịnh tiến là phép dời hình.

Nếu phép tính tiến v→ biến hai điểm M, N lần lượt thành M’, N’ thì

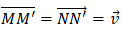
Suy ra M’N’ = MN hay phép tịnh tiến là một phép dời hình.

• Phép đối xứng trục là phép dời hình.

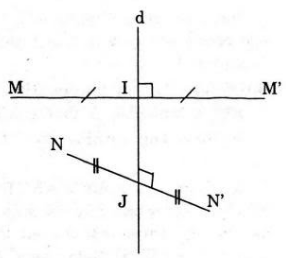
Cách 1. Gọi Đ_d là phép đối xứng qua đường thẳng d

Giả sử I là trung điểm MN’, J là trung điểm của NM’

Suy ra I, J ∈ d

Ta có:

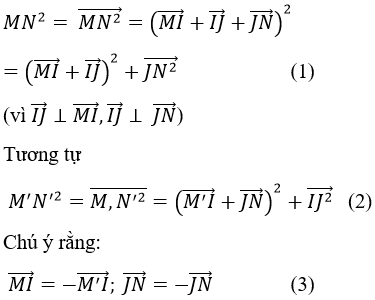
Từ (1), (2), (3) suy ra MN²=MN'²=>MN=M'N'

=> Vậy phép đối xứng trục là phép dời hình.

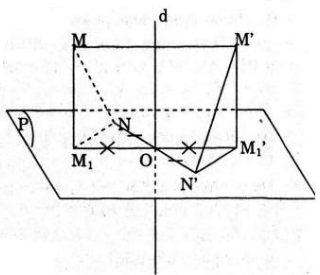
Cách 2. Giả sử phép đối xứng qua đường thẳng d biến M thành M’, N thành N’

Gọi (P) là mặt phẳng chứa NM’ và (P) // MM’

M₁,M₁' lần lượt là hình chiếu của M, M’ trên (P); O = ∩(P). Ta có d ⊥ (P) nên O đồng thời là trung điểm của M₁ M₁' và NN'. Vậy phép đối xứng tâm O biến M₁ thành M₁', N thành N’ nên M₁ M₁' nên M₁ N=M₁'N'.

Mặt khác M₁ N,M₁'N' lần lượt là hình chiếu của MN, M’N’ trên (P), MM’ // (P) nên MN = M’N’.

Vậy phép đối xứng qua đường thẳng là phép dời hình.

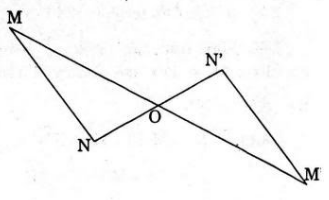
• Phép đối xứng tâm là phép dời hình.

Nếu phép đối xứng tâm O biến hai điểm M, N lần lượt thành M’, N’ thì

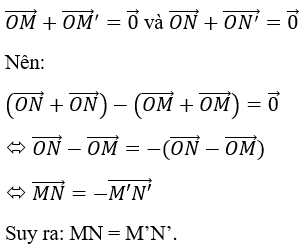
Vậy phép đối xứng tâm là phép dời hình.