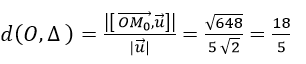Giải Đề số 2 trang 129 sgk Hình Học 12 nâng cao

---

Một số đề kiểm tra

Haylamdo biên soạn và sưu tầm lời giải Đề số 2 trang 129 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Đề số 2 (trang 129 sgk Hình Học 12 nâng cao):

Câu 1: Cho tứ diện đều ABCD cạnh bằng a. Gọi B’, C’, D’ lần lượt là trung điểm các cạnh AB, AC, AD.

a) Chứng minh rằng 6 điểm B, C, D, B’, C’, D’ nằm trên một mặt cầu. Tính bán kính mặt cầu đó?

b) Tính thể tích khối chóp D.BCC’B’

Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(2; 0; 0); A’(6; 0; 0), B(0; 3; 0); B’(0; 4; 0); C(0; 0; 4); C’(0; 0; 3).

a) Viết phương trình mặt cầu đi qua 4 bốn điểm A, A’, B, C. chứng minh rằng: B’ và C’ cùng nằm trên mặt cầu đó.

b) Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của ΔA'B'C' cùng nằm trên một đường thẳng đi qua O. Viết Phương trình đường thẳng đó.

c) Tính khoảng cách từ điểm O tới giao điểm của mp(ABC’) và (A’B’C)

Lời giải:

Câu 1:

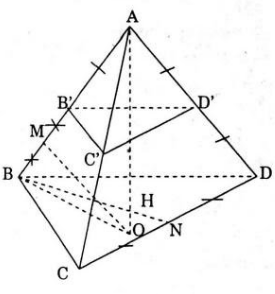
Gọi H là tâm của ΔBCD, khi đó AH ⊥ (BCD) và AH là trục đường tròn ngoại tiếp ΔB'C'D'

a) Gọi M là trung điểm BB’ và O là giao điểm của đường thẳng AH với đường trung trực OM của cạnh BB’.

Khi đó ta có:

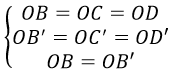
=> O cách đều 6 điểm B, C, D, B’, C’, D’ hay O là tâm mặt cầu đi qua B, C, D, B’, C’, D’. bán kính mặt cầu là R = OB.

Ta có:

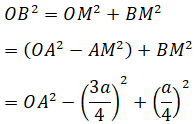
Mặt khác tam giác vuông AMO đồng dạng tam giác vuông AHB

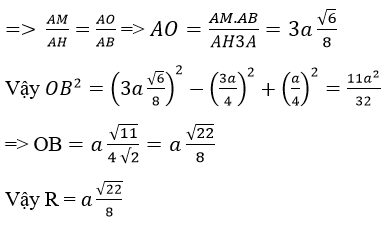
b) Tính V_D.BCC'B'. Khoảng cách từ D đến mp(ABC) cũng bằng đoạn AH (vì tứ diện ABCD đều).

Tam giác ABC có B’C’ là đường trung bình nên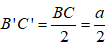 Trong mp (ABC) , kẻ AK vuông góc BC, ta có 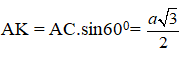Chiều cao của hình thang cân B’C’CB là: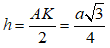

Diện tích hình thang cân B’C’CB là

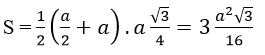
Vậy thể tích khối chóp D.BCC’B’ là:

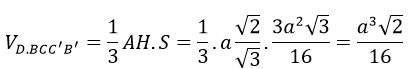
Câu 2:

a) Gọi Phương trình mặt cầu đi qua A, A’, B, C là:

x²+y²+z²+ax+by+cz+d=0

Vì mặt cầu đi qua A(2; 0; 0); A’(6; 0; 0); B(0; 3; 0), C(0; 0; 4) nên ta có hệ:

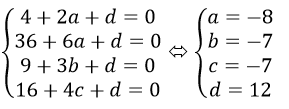
Vậy Phương trình mặt cầu là: x²+y²+z²-8x-7y-7z+12=0

Thay tọa độ điểm B’ và C' và phương trình mặt cầu thấy thỏa mãn. Do đó, các điểm B’, C’cũng nằm trên mặt cầu đó (đpcm)

b) Trực tâm H của ΔABC là

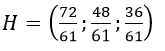
Trọng tâm G của ΔA'B'C' là

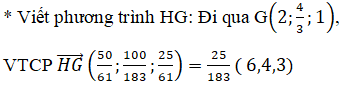
Suy ra phương trình đường thẳng HG là:

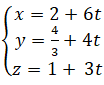
Đường thẳng này đi qua O(0; 0; 0) (khi t = -1/3). Vậy H, G, O thẳng hàng.

c) Phương trình mp(ABC’) là:

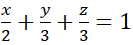
Phương trình mp(A’B’C) là:

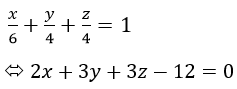
Phương trình giao tuyến của Δ của (ABC’) và (A’B’C’) là:

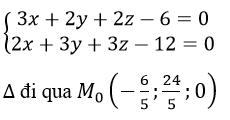
và có vectơ chỉ phương u→ =[n→,n'→ ] =(0; -5;5)

Với n→( 3;2;2),n'→(2;3;3)

Khoảng cách từ O đến Δ là