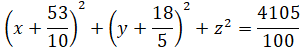Giải Đề số 3 trang 129 sgk Hình Học 12 nâng cao

Một số đề kiểm tra

Haylamdo biên soạn và sưu tầm lời giải Đề số 3 trang 130 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Đề số 3 (trang 130 sgk Hình Học 12 nâng cao):

Câu 1: Cho hình hộp ABCD.A’B’C’D’. Gọi N là điểm nằm trên cạnh AB, vì (α) là mặt phẳng đi qua 3 bốn điểm D, N, B’.

a) Mp(α) cắt hình hộp đã cho thiếu diện là hình gì?

b) Chứng minh rằng mặt phẳng (α) phần chia khối hộp đã cho thành hai khối đa diện H₁ và H₂ bằng nhau.

c) Tính tỉ số thể tích của khối đa diện H₁ và thể tích tứ diện AA’BD.

Câu 2: Trong không gian tọa độ Oxyz cho các điểm: A(1; -3; -1); và B(-2; 1; 3)

a) Chứng tỏ rằng hai điểm A và B cách đều trục Ox.

b) Tìm điểm C nằm trên Oz sao cho tam giác ABC vuông tại C.

c) Viết phương trình hình chiếu của đường thẳng AB trên mp(Oyz).

d) Viết phương trình mặt cầu đi qua ba điểm O, A, B và có tâm nằm trên mp(Oyz).

Lời giải:

Câu 1:

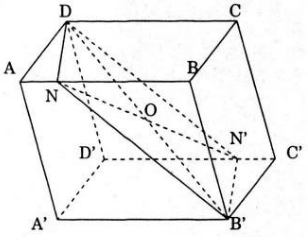
a) Vì số mặt phẳng cắt mặt phẳng song song theo hai giao tuyến song song nên α cắt hình hộp theo thiết diện là hình bình hành DNB’N’.

b) H₁ và H₂ là hai hình đa diện đối xứng với nhau qua tâm O của hình hộp nên chúng bằng nhau.

c) Vì H₁ và H₂ bằng nhau nên thể tích của chúng bằng một thể tích hình hộp.

Mặt khác

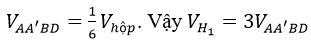
Câu 2:

a) Ta có:

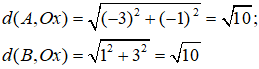
⇒ d(A,Ox)=d(B,Ox)=√10 (đpcm)

b) Gọi C(0; 0; c) ∈Oz là điểm cần tìm.

Vì ΔABC vuông tại C nên CA²+CB²=AB²

<=> 1+9+(1+c)²+4+1+(3-c)²=9+16+16

<=> 2c²-4c-16=0 <=> c = 4 và c = -2

Vậy điểm C thỏa mãn bài toàn là: C = (0; 0; 4) và C’(0; 0; -2)

c) Hình chiếu của A(1; -3; -1) lên mp(Oyz) là A’(0; -3; -1)

Hình chiếu của B(-2; 1; 3) lên mp(Oyz) là B’(0; 1; 3)

Vậy A’B’ chính là hình chiếu của AB lên mp(Oyz).

Đường thẳng A’B’ qua A’(0, -3; -1) và nhận VTCP A'B'→= (0, 4, 3)

Phương trình đường thẳng A’B’ là:

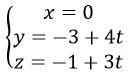
d) Gọi I(a; b; 0) ∈ (Oxy) là tâm của mặt cầu đi qua O, A, B.

Khi đó ta có:

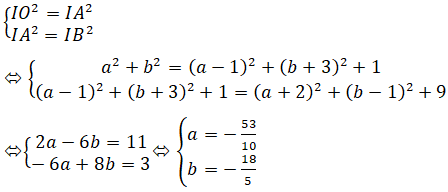
Vậy phương trình mặt cầu là: