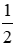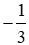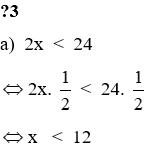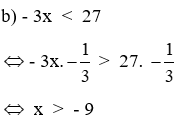Giáo án Toán 8 Bài 4: Bất phương trình bậc nhất một ẩn mới nhất

1. KHỞI ĐỘNG

- Để hiểu thế nào là BPT bậc nhất 1 ẩn, biết áp dụng từng quy tắc biến đổi BPT để giải BPT.

- Biết áp dụng từng quy tắc biến đổi BPT để giải thích sự tương đương của BPT.

Chúng ta sẽ cùng tìm hiểu bài học hôm nay.

2. HÌNH THÀNH KIẾN THỨC

Hoạt động 2: Tìm hiểu định nghĩa. (9 phút).

- Phương trình bậc nhất một ẩn có dạng như thế nào?

- Nếu thay dấu “=” bởi dấu “ > ”, “ < ”, “≤”, “≥” thì lúc này ta được bất phương trình.

- Hãy định nghĩa bất phương trình bậc nhất một ẩn.

- Treo bảng phụ ?1 và cho học sinh thực hiện.

- Vì sao 0x + 5 > 0 không phải là bất phương trình bậc nhất một ẩn?

- Phương trình bậc nhất một ẩn có dạng ax+b = 0 (a ≠ 0)

- HS: Nêu định nghĩa như SGK

- Đọc và thực hiện ?1

0x+5 > 0 không phải là bất phương trình bậc nhất một ẩn, vì a = 0

1. Định nghĩa.

Bất phương trình dạng ax +b < 0 (hoặc ax + b  >  0, ax + b ≤ 0, ax + b ≥ 0), trong đó a và b là hai số đã cho, a ≠ 0, được gọi là bất phương trình bậc nhất một ẩn.

?1 Các bất phương trình bậc nhất một ẩn là:

a) 2x-3 < 0;         

c) 5x-150

Hoạt động 3: Hai quy tắc biến đổi bất phương trình. (19 phút).

- Nhắc lại hai quy tắc biến đổi phương trình.

- Tương tự, hãy phát biểu quy tắc chuyển vế trong bất phương trình?

- Ví dụ:  x-5 < 18 ⇔ x < 18 ?....

⇔ x < ...

- Treo bảng phụ ?2 và cho học sinh thực hiện.

- Nhận xét, sửa sai.

- Hãy nêu tính chất liên hệ giữa thứ tự và phép nhân.

- Hãy phát biểu quy tắc nhân với một số.

- Treo bảng phụ giới thiệu ví dụ 3, 4 cho học sinh hiểu.

- Treo bảng phụ ?3

- Câu a) ta nhân hai vế của bất phương trình với số nào?

- Câu b) ta nhân hai vế của bất phương trình với số nào?

- Khi nhân hai vế của bất phương trình với số âm ta phải làm gì?

- Hãy hoàn thành lời giải

- Nhận xét, sửa sai.

- Treo bảng phụ ?4

- Hai bất phương trình gọi là tương đương khi nào?

- Vậy để giải thích sự tương đương ta phải làm gì?

- Nhận xét, sửa sai.

- Lắng nghe.

- Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta phải đổi dấu hạng tử đó.

⇔ x < 18 + 5

⇔ x <  23

- Đọc và thực hiện ?2

- Lắng nghe, ghi bài.

- Nêu tính chất liên hệ giữa thứ tự và phép nhân đã học.

- Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:  

+ Giữ nguyên chiều bất phương trình nếu số đó dương;

+ Đổi chiều bất phương trình nếu số đó âm.

- Quan sát, lắng nghe.

- Đọc yêu cầu ?3

- Câu a) ta nhân hai vế của bất phương trình với số

- Câu b) ta nhân hai vế của bất phương trình với số

- Khi nhân hai vế của bất phương trình với số âm ta phải đổi chiều bất phương trình.

- Thực hiện

- Lắng nghe, ghi bài.

- Đọc yêu cầu ?4

- Hai bất phương trình gọi là tương đương khi chúng có cùng tập  nghiệm.

- Tìm tập nghiệp của chúng rồi kết luận.

- Lắng nghe, ghi bài.

2. Hai quy tắc biến đổi bất phương trình.

a) Quy tắc chuyển vế:

(SGK)

Ví dụ 1:  (SGK)

Ví dụ 2:  (SGK)

?2a)  x + 12  >  21

⇔ x  >  21 – 12 ⇔ x  >  9

Vậy tập nghiệm của bất phương trình là {x / x  >  9}

b)  - 2x  >  - 3x - 5

⇔ -2x + 3x   >  - 5 ⇔ x  >  - 5

Vậy tập nghiệm của bất phương trình là {x / x  >  -5}

b) Quy tắc nhân với một số.

Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:  

- Giữ nguyên chiều bất phương trình nếu số đó dương;

- Đổi chiều bất phương trình nếu số đó âm.

Ví dụ 3:  (SGK)

Ví dụ 4:  (SGK)

Vậy tập nghiệm của bất phương trình là {x / x  <  12}

Vậy tập nghiệm của bất phương trình là {x / x  >  -9}

?4 Giải thích sự tương đương:

⇔ x + 3 < 7 x - 2 < 2

Ta có:   x + 3 < 7 ⇔ x < 4

              x - 2 < 2 ⇔ x < 4

Vậy hai bất phương trình trên tương đương với nhau vì có cùng tập nghiệp.

3. LUYỆN TẬP

Bài tập 19 trang 47 SGK.

- Nhận xét, sửa sai.

- Đọc và thực hiện.

- Lắng nghe, ghi bài.

Bài tập 19 trang 47 SGK.

a) x - 5 > 3 ⇔ x > 3 + 5 ⇔ x > 8

Vậy tập nghiệm của bất phương trình là {x / x  >  6}

b) x - 2x < -2x + 4 ⇔ x < 4

Vậy tập nghiệm của bất phương trình là {x / x  <  4}

4. VẬN DỤNG

Hãy nhắc lại tính chất về liên hệ giữa thứ tự và phép cộng, tính chất về liên hệ giữa thứ tự và phép nhân.

* Làm bài tập phần vận dụng

5. MỞ RỘNG

Vẽ sơ đồ tư duy khái quát nội dung bài học.

Sưu tầm và làm một số bài tập nâng cao.

Làm bài tập phần mở rộng.