Giải SBT Toán 10 trang 105 Tập 1 Cánh diều

❮ Bài trước Bài sau ❯

Với Giải sách bài tập Toán 10 trang 105 Tập 1 trong Bài 6: Tích vô hướng của hai vectơ SBT Toán 10 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 105.

Giải SBT Toán 10 trang 105 Tập 1 Cánh diều

Bài 57 trang 105 SBT Toán 10 Tập 1: Cho tam giác ABC. Giá trị của $\vec{B A} . \vec{C A}$ bằng:

A. AB . AC . cos $\hat{B A C}$ .

B. – AB . AC . cos $\hat{B A C}$ .

C. AB . AC . cos $\hat{A B C}$ .

D. AB . AC . cos $\hat{A B C}$ .

Lời giải:

Đáp án đúng là A

Xét tam giác ABC, có: $\vec{B A} . \vec{C A} = (- \vec{A B}) . (- \vec{A C}) = B A . C A . c os (- \vec{A B}, - \vec{A C})$

= $B A . C A . c os \hat{B A C}$

= $B A . C A . c os (\hat{B A C})$

Vậy chọn A.

Bài 58 trang 105 SBT Toán 10 Tập 1: Cho tam giác ABC. Giá trị của $\vec{A B} . \vec{B C}$ bằng:

A. AB . BC . cos $\hat{A B C}$ .

B. AB . AC . cos $\hat{A B C}$ .

C. – AB . BC . cos $\hat{A B C}$ .

D. AB . BC . cos $\hat{B A C}$ .

Lời giải:

Đáp án đúng là A

$\vec{A B} . \vec{B C} = - \vec{B A} . \vec{B C} = - A B . B C . \cos (- \vec{B A}, \vec{B C})$

= $- A B . B C . \cos (180 ° - \hat{A B C})$

= $A B . B C . \cos \hat{A B C}$

Vậy chọn A.

Bài 59 trang 105 SBT Toán 10 Tập 1: Cho đoạn thẳng AB. Tập hợp các điểm M nằm trong mặt phẳng thỏa mãn $\vec{M A} . \vec{M B} = 0$ là:

A. Đường tròn tâm A bán kính AB.

B. Đường tròn tâm B bán kính AB.

C. Đường trung trực của đoạn thẳng AB.

D. Đường tròn đường kính AB.

Lời giải:

Đáp án đúng là D

Ta có: $\vec{M A} . \vec{M B} = 0$

⇒ $\hat{(\vec{M A}; \vec{M B})} = \hat{A M B} = 90 °$

Do đó tập hợp các điểm M thỏa mãn $\hat{A M B} = 90 °$ là đường tròn đường kính AB.

Bài 60 trang 105 SBT Toán 10 Tập 1: Nếu hai điểm M và N thỏa mãn $\vec{M N} . \vec{N M} = - 9$ thì:

A. MN = 9.

B. MN = 3.

C. MN = 81.

D. MN = 6.

Lời giải:

Đáp án đúng là B

Ta có: $\vec{M N} . \vec{N M} = M N . M N . c o s (\vec{M N}, \vec{N M}) = M N . M N . c o s 180 ° = - M N^{2}$

Mà $\vec{M N} . \vec{N M} = - 9$ nên – MN² = – 9 ⇔ MN² = 9 ⇔ MN = 3 (thỏa mãn) hoặc MN = – 3 (không thỏa mãn).

Vậy MN = 3.

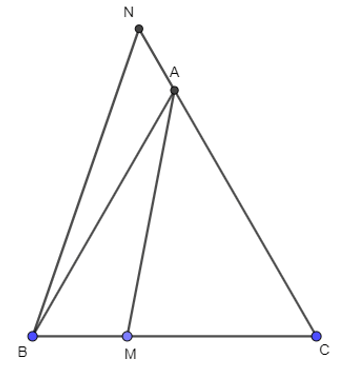
Bài 61 trang 105 SBT Toán 10 Tập 1: Cho tam giác ABC đều cạnh a. Các điểm M, N lần lượt thuộc các tia BC và CA thỏa mãn $B M = \frac{1}{3} B C$ , $C N = \frac{5}{4} C A$ . Tính:

a) $\vec{A B} . \vec{A C}, \vec{A M} . \vec{B N}$ .

b) MN.

Lời giải:

Cho tam giác ABC đều cạnh a. Các điểm M, N lần lượt thuộc các tia BC và CA thỏa mãn BM = 1/3 BC, CN = 5/4 CA

a) Ta có: $\vec{A B} . \vec{A C} = A B . A C . c o s (\vec{A B}, \vec{A C})$

= $A B . A C . \cos \hat{B A C}$

= $a . a . \cos 60 °$

= $\frac{1}{2} a^{2}$

$\vec{A M} . \vec{B N} = (\vec{A B} + \vec{B M}) . (\vec{B A} + \vec{A N})$

$= (\vec{A B} + \frac{1}{3} \vec{B C}) . (\frac{1}{4} \vec{C A} - \vec{A B})$

$= (\vec{A B} + \frac{1}{3} (\vec{A C} - \vec{A B})) . (- \frac{1}{4} \vec{A C} - \vec{A B})$

$= (\frac{2}{3} \vec{A B} + \frac{1}{3} \vec{A C}) . (- \frac{1}{4} \vec{A C} - \vec{A B})$

$= - \frac{2}{3} \vec{A B} . \frac{1}{4} \vec{A C} - \frac{2}{3} \vec{A B} . \vec{A B} - \frac{1}{3} \vec{A C} . \frac{1}{4} \vec{A C} - \frac{1}{3} \vec{A C} . \vec{A B}$ $= - \frac{1}{6} \vec{A B} . \vec{A C} - \frac{2}{3} {\vec{A B}}^{2} - \frac{1}{12} {\vec{A C}}^{2} - \frac{1}{3} \vec{A C} . \vec{A B}$

$= - \frac{1}{6} . \frac{1}{2} a^{2} - \frac{2}{3} . a^{2} - \frac{1}{12} . a^{2} - \frac{1}{3} . \frac{1}{2} a^{2}$

$= - \frac{1}{12} a^{2} - \frac{2}{3} . a^{2} - \frac{1}{12} . a^{2} - \frac{1}{6} a^{2}$

$= - a^{2}$ .

b) Ta có: $\vec{M N} = \vec{M C} + \vec{C N}$

⇔ $\vec{M N} = \vec{M B} + \vec{B C} + \vec{C N} = - \frac{1}{3} \vec{B C} + \vec{B C} + \frac{5}{4} \vec{C A} = \frac{2}{3} \vec{B C} + \frac{5}{4} \vec{C A}$

⇔ ${\vec{M N}}^{2} = {(\frac{2}{3} \vec{B C} + \frac{5}{4} \vec{C A})}^{2}$

⇔ ${\vec{M N}}^{2} = {(\frac{2}{3} \vec{B C})}^{2} + \frac{5}{3} \vec{B C} . \vec{C A} + {(\frac{5}{4} \vec{C A})}^{2}$

⇔ ${\vec{M N}}^{2} = {(\frac{2}{3} \vec{B C})}^{2} - \frac{5}{3} \vec{C B} . \vec{C A} + {(\frac{5}{4} \vec{C A})}^{2}$

⇔ ${\vec{M N}}^{2} = \frac{4}{9} {\vec{B C}}^{2} - \frac{5}{3} | \vec{B C} | . | \vec{C A} | cos (\vec{C B}, \vec{C A}) + \frac{25}{16} {\vec{C A}}^{2}$

⇔ ${\vec{M N}}^{2} = \frac{4}{9} {\vec{B C}}^{2} - \frac{5}{3} | \vec{B C} | . | \vec{C A} | cos \hat{C B A} + \frac{25}{16} {\vec{C A}}^{2}$

⇔ ${\vec{M N}}^{2} = \frac{4}{9} a^{2} - \frac{5}{3} a . a cos60 ° + \frac{25}{16} a^{2}$

⇔ ${\vec{M N}}^{2} = \frac{4}{9} a^{2} - \frac{5}{6} a^{2} + \frac{25}{16} a^{2} = \frac{169}{144} a^{2}$

⇔ $M N = \frac{13}{12} a$

Vậy $M N = \frac{13}{12} a$ .

Lời giải Sách bài tập Toán Cánh diều 10 Bài 6: Tích vô hướng của hai vectơ Cánh diều hay khác:

Giải SBT Toán 10 trang 106 Tập 1

Xem thêm lời giải Sách bài tập Toán 10 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯