Giải SBT Toán 10 trang 32 Tập 1 Cánh diều

---

Với Giải sách bài tập Toán 10 trang 32 Tập 1 trong Bài tập cuối chương 2 trang 31,32,33 SBT Toán 10 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 32.

Giải SBT Toán 10 trang 32 Tập 1 Cánh diều

Bài 24 trang 32 SBT Toán 10 Tập 1:

Giá trị nhỏ nhất của biểu thức F = – 2x + y trên miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-y\ge -2\\ x+y\le 4\\ x-5y\le -2\end{array}\right.$ là:

A. – 5.

B. – 7.

C. 1.

D. 4.

Lời giải:

Đáp án đúng là A

Xác định miền nghiệm của hệ bất phương trình như sau:

- Vẽ ba đường thẳng:

Đường thẳng d₁: x – y = – 2 cắt trục Ox, Oy lần lượt tại các điểm có tọa độ (– 2; 0) và (0; 2).

Đường thẳng d₂: x + y = 4 cắt trục Ox, Oy lần lượt tại các điểm có tọa độ (4; 0) và (0; 4).

Đường thẳng d₃: x – 5y = – 2 lần lượt đi qua các điểm có tọa độ (– 2; 0) và (3; 1).

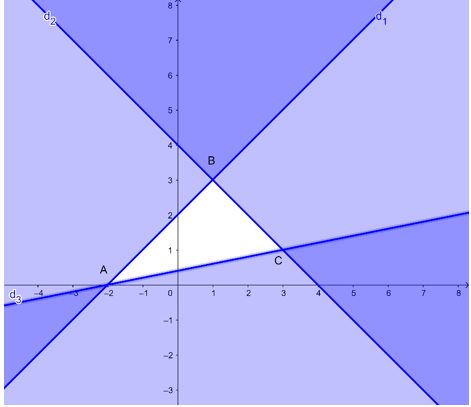
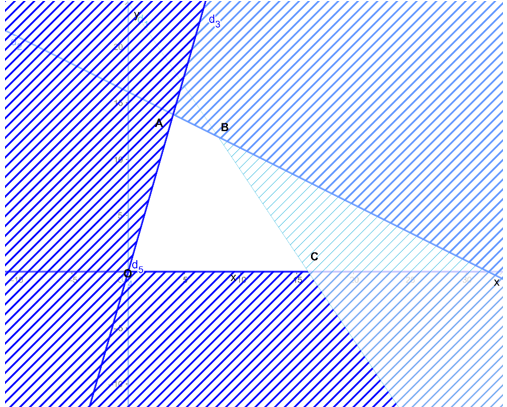
- Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình. Miền nghiệm của hệ bất phương trình là miền trong tam giác ABC với A( – 2; 0), B(1; 3) và C(3; 1) như hình vẽ sau:

Ta có biểu thức F = – 2x + y  có giá trị nhỏ nhất tại một trong các đỉnh của tam giác ABC.

Tính giá trị biểu thức T tại các đỉnh của tứ giác:

Tại A(– 2; 0), với x = – 2 và y = 0 thì F = – 2.(– 2) + 0 = 4;

Tại B(1; 3), với x = 1 và y = 3 thì F = – 2.1 + 3 = 1;

Tại C(3; 1), với x = 3 và y = 1 thì F = – 2.3 + 1 = – 5 ;

Ta được F đạt giá trị nhỏ nhất bằng – 5 khi x = 3, y = 1.

Bài 25 trang 32 SBT Toán 10 Tập 1: Biểu diễn miền nghiệm của các bất phương trình sau:

a) 3x > 2;

b) 2y ≤ – 5;

c) 2x – y ≥ 1;

d) 3x – 2y < 5.

Lời giải:

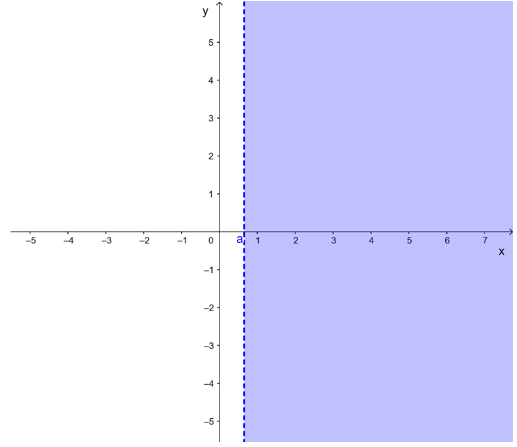
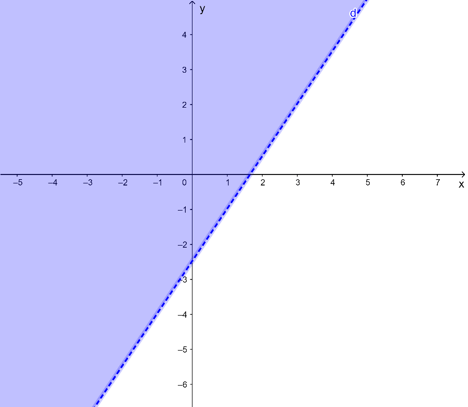
a) Vẽ đường thẳng a: 3x = 2

Lấy O(0; 0) có 3.0 = 0 < 2.

Do đó miền nghiệm của bất phương trình không chứa điểm O và không kể đường thẳng a được là phần tô màu xanh trong hình vẽ sau:

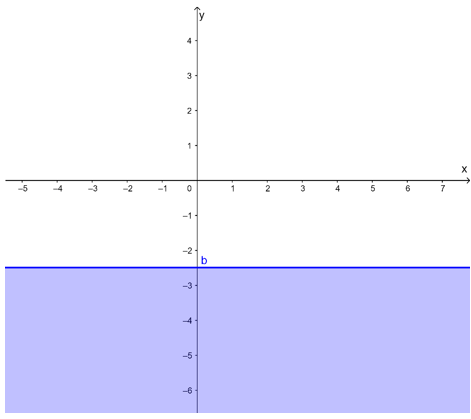
b) Vẽ đường thẳng b: 2y = – 5

Lấy O(0; 0) có 2.0 = 0 > – 5.

Do đó miền nghiệm của bất phương trình không chứa điểm O và kể đường thẳng b được biểu diễn trong hình vẽ sau:

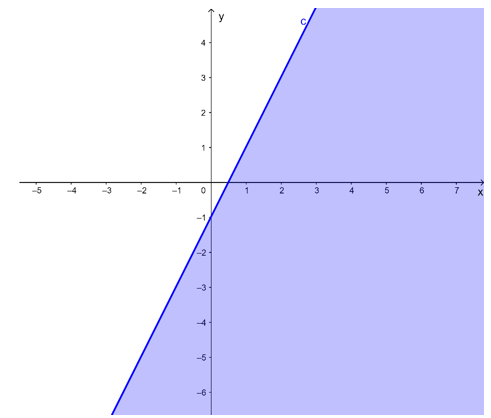
c) Vẽ đường thẳng c: 2x – y = 1

Lấy O(0; 0) có 2.0 – 0 = 0 < 1.

Do đó miền nghiệm của bất phương trình không chứa điểm O và kể cả đường thẳng c được biểu diễn bởi phần tô màu trong hình vẽ sau:

d) Vẽ đường thẳng d: 3x – 2y = 5

Lấy O(0; 0) có 3.0 – 2.0 = 0 < 5.

Do đó miền nghiệm của bất phương trình không chứa điểm O và không kể đường thẳng d được biểu diễn bởi phần tô màu trong hình vẽ sau:

Bài 26 trang 32 SBT Toán 10 Tập 1: Biểu diễn miền nghiệm của các hệ bất phương trình sau:

a) $\left\{\begin{array}{l}x-3y<0\\ x+2y>-3\\ x+y<2\end{array}\right.$

b) $\left\{\begin{array}{l}x-2y\le 3\\ 3x+2y\ge 9\\ x+y\le 6\\ x\ge 1\end{array}\right.$

c)$\left\{\begin{array}{l}x+2y\le 2\\ x+2y\ge -2\\ x-2y\le 2\\ x-2y\ge -2\end{array}\right.$

Lời giải:

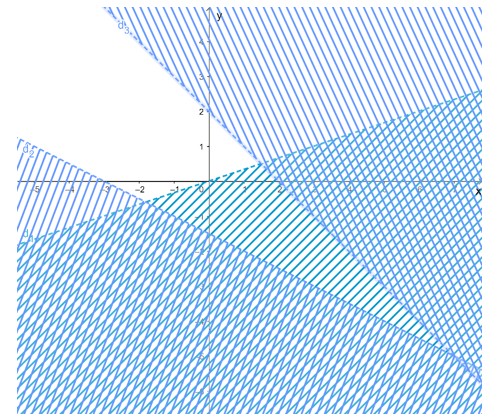
a) Vẽ các đường thẳng:

d₁: x – 3y = 0 là đường thẳng đi qua hai điểm có tọa độ là (0; 0) và (3; 1).

d₂: x + 2y = – 3 là đường thẳng đi qua hai điểm (– 3; 0) và (1; – 2).

d₃: x + y = 2 là đường thẳng đi qua hai điểm (2; 0) và (0; 2).

Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình trong hệ ta được miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình dưới đây:

 b) Vẽ các đường thẳng:

d₁: x – 2y = 3 là đường thẳng đi qua hai điểm có tọa độ là (3; 0) và (1; – 1).

d₂: 3x + 2y = 9 là đường thẳng đi qua hai điểm (3; 0) và (1; 3).

d₃: x + y = 6 là đường thẳng đi qua hai điểm (6; 0) và (0; 6).

d₄: x + y = 6 là đường thẳng song song với trục tung Oy và đi qua điểm (1; 0).

Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình trong hệ ta được miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình dưới đây:

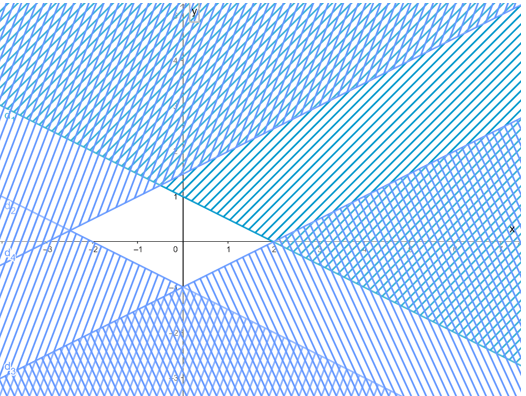
 c) Vẽ các đường thẳng:

d₁: x + 2y = 2 là đường thẳng đi qua hai điểm có tọa độ là (2; 0) và (0; 1).

d₂: x + 2y = – 2 là đường thẳng đi qua hai điểm (– 2 ; 0) và (0; – 1).

d₃: x – 2y = 2 là đường thẳng đi qua hai điểm (2; 0) và (0;  – 1).

d₄: x – 2y = – 2  là đường thẳng đi qua hai điểm (–2; 0) và (0; 1).

Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình trong hệ ta được miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình dưới đây:

Bài 27 trang 32 SBT Toán 10 Tập 1:

a) Biểu diễn miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}3x-y\le 9\\ 3x+6y\le 30\\ x\ge 0\\ 0\le y\le 4\end{array}\right.$(I).

b) Tìm x, y là nghiệm của hệ bất phương trình (I) sao cho F = 3x + 4y đạt giá trị lớn nhất.

Lời giải:

Vẽ các đường thẳng:

d1: 3x – y = 9 là đường thẳng đi qua hai điểm có tọa độ là (3; 0) và (0; 9).

d₂: 3x + 6y = 30 là đường thẳng đi qua hai điểm (10; 0) và (0; 5).

d₃: x = 0 là trục tung.

d₄: y = 0 là trục hoành

d₅: y = 4 là đường thẳng đi qua điểm (0; 4) và song song với trục hoành.

Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình trong hệ ta được miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình dưới đây chính là miền ngũ giác OABCD với O(0; 0), A(0; 4), B(2; 4), C(4; 3), D(3; 0):

b) Biểu thức F = 3x + 4y đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác OABCD.

Tính giá trị biểu thức F tại các điểm, ta được:

Tại O(0; 0) với x = 0 và y = 0 thì F = 3.0 + 4.0 = 0;

Tại A(0; 4) với x = 0 và y = 4 thì F = 3.0 + 4.4 = 16;

Tại B(2; 4) với x = 2 và y = 4 thì F = 3.2 + 4.4 = 22;

Tại C(4; 3) với x = 4 và y = 3 thì F = 3.4 + 4.3 = 24;

Tại D(3; 0) với x = 3 và y = 0 thì F = 3.3 + 4.0 = 9.

Từ đó giá trị lớn nhất của F là 24 với x = 4 và y = 3.

Vậy giá trị lớn nhất của F bằng 24 khi x = 4 và y = 3.

Bài 28 trang 32 SBT Toán 10 Tập 1: Một sân bóng đá được tổ chức tại một sân vận động có sức chứa 40 000 người, ban tổ chức phát hành hai loại vé là 400 000 đồng và 200 000 đồng. Do điều kiện sân đấu nên số lượng vé 400 000 đồng không lớn hơn số lượng vé 200 000 đồng. Để an toàn phòng dịch, liên đoàn bóng đá yêu cầu số lượng vé không vượt quá 30% sức chứa của sân. Để tổ chức được trận đấu thì số tiền thu được thông qua bán vé không được ít hơn 3 tỉ đồng. Gọi x, y lần lượt là số vé vé 400 000 đồng và 200 000 đồng được bán ra.

a) Viết hệ bất phương trình bậc nhất hai ẩn x, y để biển diễn số lượng vé mỗi loại được bán ra đảm bảo mục đích của ban tổ chức.

b) Chỉ ra hai nghiệm của hệ bất phương trình đó.

Lời giải:

Gọi x, y lần lượt là số vé vé 400 000 đồng và 200 000 đồng được bán ra (x, y ∈ ℕ^*).

30% sức chứa của sân là: 30%.40 000 = 12 000 (người)

Để an toàn phòng dịch số lượng vé không vượt quá 30% sức chứa của sân nên ta có: x + y ≤ 12 000 (1).

Do điều kiện sân đấu nên số lượng vé 400 000 đồng không lớn hơn số lượng vé 200 000 đồng do đó x ≤ y hay x – y ≤ 0 (2).

Số tiền thu được thông quan bán vé không được ít hơn 3 tỉ đồng nên ta có:

400 000x + 200 000y ≥ 3 000 000 000 hay 2x + y ≥ 15 000 (3).

Từ (1), (2), (3) và điều kiện của x và y ta có hệ bất phương trình: $\left\{\begin{array}{l}x+y\le 12000\\ x-y\le 0\\ 2x+y\ge 15000\\ x\ge 0\\ y\ge 0\end{array}\right.$

b) Chọn x = 5 000 và y = 5 000, ta thấy cặp số này thỏa mãn tất cả các bất phương trình trong hệ nên (5 000; 5 000) là nghiệm của hệ bất phương trình.

Chọn x = 4 000 và y = 7 000, ta thấy cặp số này thỏa mãn tất cả các bất phương trình trong hệ nên (4 000; 7 000) là nghiệm của hệ bất phương trình

Bài 29 trang 32 SBT Toán 10 Tập 1: Một xưởng sản xuất bàn và ghế. Một chiếc bàn cần 1,5 giờ lắp ráp và 1 giờ để hoàn thiện; một chiếc ghế cần 1 giờ để lắp ráp và 2 giờ để hoàn thiện. Bộ phận lắp ráp có 3 nhân công, bộ phận hoàn thiện có 4 nhân công. Biết thị trường luôn tiêu thụ hết sản phẩm của xưởng và lượng ghế tiêu thụ không vượt quá 3,5 lần số bàn.

a) Viết hệ bất phương trình mô tả số lượng bàn và ghế mà trong một ngày phân xưởng có thể sản xuất, biết một nhân công làm việc không quá 8 tiếng mỗi ngày.

b) Biểu diễn miền nghiệm của hệ bất phương trình đó.

c) Biết một chiếc bàn lãi 600 nghìn đồng, một chiếc ghế lãi 450 nghìn đồng. Hỏi trong một ngày, xưởng cần sản xuất bao nhiêu chiếc bàn, bao nhiêu chiếc ghế để thu được tiền lãi cao nhất.

Lời giải:

Gọi số bàn xưởng sản xuất được là x (bàn) và số ghế xưởng sản xuất được là y (ghế) (x, y ∈ ℕ).

Xưởng có 3 công nhân lắp ráp và một công nhân làm việc không quá 8 tiếng mỗi ngày nên tổng thời gian lắp ráp một ngày là 3.8 = 24 (giờ).

Xưởng có 4 công nhân hoàn thiện và một công nhân làm việc không quá 8 tiếng mỗi ngày nên tổng thời gian lắp ráp một ngày là: 4.8  =32 (giờ).

Tổng thời gian lắp ráp x chiếc bàn và y chiếc ghế không vượt quá 24 giờ nên: 1,5x + y ≤ 24 (1).

Tổng thời gian hoàn thiện x chiếc bàn và y chiếc ghế không vượt quá 32 giờ nên: x + 2y ≤ 32 (2).

Vì lượng ghế tiêu thụ không vượt quá 3,5 lần số bàn nên 3,5x ≥ y (3).

Từ (1), (2), (3) và điều kiện của x, y nên ta có hệ bất phương trình sau: $\left\{\begin{array}{l}1,5x+y\le 24\\ x+2y\le 30\\ 3,5x-y\ge 0\\ x\ge 0\\ y\ge 0\end{array}\right.$

b) Vẽ các đường thẳng sau:

d₁: 1,5x + y = 24 là đường thẳng đi qua hai điểm (16; 0) và (0; 24).

d₂: x + 2y = 32 là đường thẳng đi qua hai điểm (32; 0) và (0; 16).

d₃: 3,5x – y = 0 là đường thẳng đi qua hai điểm (0; 0) và (2; 7).

d₄: x = 0 là trục Oy.

d₅: y = 0 là trục Ox.

Gạch đi các phần không thuộc miền nghiệm của từng bất phương trình ta được miền nghiệm của hệ bất phương trình là miền trong tứ giác OABC với O(0; 0), A(4; 14), B(8; 12), C(16; 0).

c) Số tiền lãi mà phân xưởng thu được khi bán x chiếc bàn và y chiếc ghế là: 600x + 450y (nghìn đồng).

Đặt T = 600x + 450y.

Biểu thức T = 600x + 450y đạt giá trị lớn nhất tại các đỉnh của tứ giác OABC.

Tính giá trị biểu thức T tại các đỉnh ta được:

Tại O(0; 0) với x = 0, y = 0 thì T = 600.0 + 450.0 = 0;

Tại A(4; 14) với x = 4, y = 14 thì T = 600.4 + 450.14 = 8 700;

Tại B(8; 12) với x = 8, y = 12 thì T = 600.8 + 450.12 = 10 200;

Tại C(16; 0) với x = 16, y = 0 thì T = 600.16 + 450.0 = 9 600.

Suy ra T đạt giá trị lớn nhất bằng 10 200 khi x = 8 và y = 12.

Vậy xưởng cần sản xuất 8 chiếc bàn và 12 chiếc ghế để thu được tiền lãi lớn nhất là 10 200 000 đồng.

Lời giải Sách bài tập Toán Cánh diều 10 Bài tập cuối chương 2 trang 31,32,33 Cánh diều hay khác:

• Giải SBT Toán 10 trang 31 Tập 1

• Giải SBT Toán 10 trang 33 Tập 1