Cho bất phương trình bậc nhất hai ẩn: 2x – 5y + 10 > 0
Giải SBT Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn
Haylamdo biên soạn và sưu tầm lời giải Bài 1 trang 27 SBT Toán 10 Tập 1 trong Bài 1: Bất phương trình bậc nhất hai ẩn. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.
Bài 1 trang 27 SBT Toán 10 Tập 1: Cho bất phương trình bậc nhất hai ẩn: 2x – 5y + 10 > 0.
a) Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng Oxy.
b) (1; 3) có phải là nghiệm của bất phương trình trên không?
c) Chỉ ra 2 cặp số (x; y) thỏa mãn bất phương trình trên.
Lời giải:
a) Vẽ đường thẳng 2x – 5y + 10 = 0.
Cho x = 0, khi đó 2 . 0 – 5y + 10 = 0, suy ra y = 2.
Cho y = 0, khi đó 2x – 5 . 0 + 10 = 0, suy ra x = – 5.
Do đó, đường thẳng 2x – 5y + 10 = 0 đi qua hai điểm (0; 2) và (– 5; 0).
Lấy điểm O(0; 0) không thuộc đường thẳng 2x – 5y + 10 = 0.
Ta có: 2 . 0 – 5 . 0 + 10 = 10 > 0, do đó tọa độ điểm O thỏa mãn bất phương trình 2x – 5y + 10 > 0.
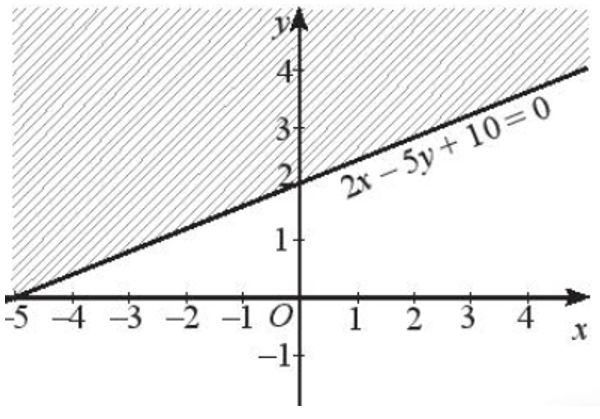
Vậy miền nghiệm của bất phương trình 2x – 5y + 10 > 0 là nửa mặt phẳng có bờ là đường thẳng 2x – 5y + 10 = 0, chứa gốc O và không kể đường thẳng 2x – 5y + 10 = 0 (miền không bị gạch trong hình dưới đây).
b) Thay x = 1, y = 3 vào biểu thức 2x – 5y + 10, ta được:
2 . 1 – 5 . 3 + 10 = – 3 < 0
Do đó, cặp số (1; 3) không thỏa mãn bất phương trình 2x – 5y + 10 > 0.
Vậy (1; 3) không là nghiệm của bất phương trình đã cho.
c) Ta chọn cặp số (x; y) tùy ý sao cho 2x – 5y + 10 > 0.
Chẳng hạn các cặp số (1; 2) và (3; 3) thỏa mãn bất phương trình đã cho.
Do 2 . 1 – 5 . 2 + 10 = 2 > 0 và 2 . 3 – 5 . 3 + 10 = 1 > 0.