Một lớp học có 36 học sinh, trong đó 20 người thích bóng rổ, 14 người thích bóng bàn

Giải SBT Toán 10 Bài tập cuối chương 1

Haylamdo biên soạn và sưu tầm lời giải Bài 4 trang 19 SBT Toán 10 Tập 1 trong Bài tập cuối chương 1. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Bài 4 trang 19 SBT Toán 10 Tập 1: Một lớp học có 36 học sinh, trong đó 20 người thích bóng rổ, 14 người thích bóng bàn và 10 người không thích môn nào trong hai môn thể thao này.

a) Có bao nhiêu học sinh của lớp thích cả hai môn trên?

b) Có bao nhiêu học sinh của lớp thích bóng rổ nhưng không thích bóng bàn?

Lời giải:

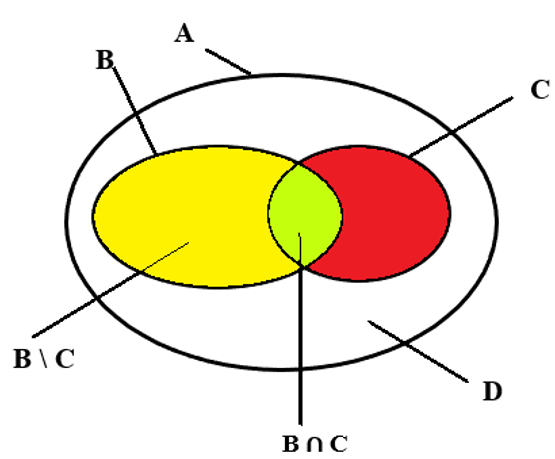
Kí hiệu A là tập hợp các học sinh của lớp, B = {x ∈ A | x thích bóng rổ},

C = {x ∈ A | x thích bóng bàn}, D = {x ∈ A | x không thích môn nào trong hai môn}.

Theo giả thiết, ta có: n(A) = 36, n(B) = 20, n(C) = 14 và n(D) = 10.

a) Số học sinh thích một trong hai môn là:

n(B ∪ C) = n(A) – n(D) = 36 – 10 = 26 (bạn).

Số học sinh thích cả hai môn thể thao trên là:

n(B ∩ C) = n(B) + n(C) – n(B ∪ C) = 20 + 14 – 26 = 8 (bạn).

b) Số học sinh thích bóng rổ nhưng không thích bóng bàn là:

n(B \ C) = n(B) – n(B ∩ C) = 20 – 8 = 12 (bạn).