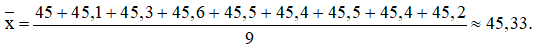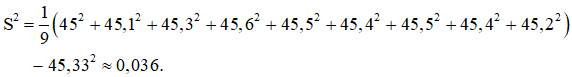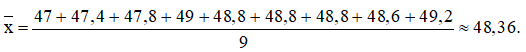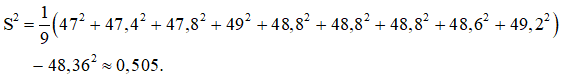Bảng sau ghi giá bán ra lúc 11 giờ trưa của 2 mã cổ phiếu A và B SBT Toán 10 Tập 1

Haylamdo biên soạn và sưu tầm lời giải Bài 6 trang 130 SBT Toán 10 Tập 1 trong Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

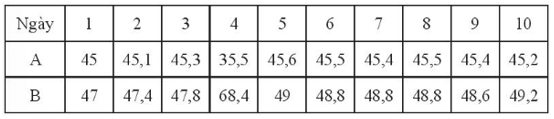
Bài 6 trang 130 SBT Toán 10 Tập 1: Bảng sau ghi giá bán ra lúc 11 giờ trưa của 2 mã cổ phiếu A và B trong 10 ngày liên tiếp (đơn vị: nghìn đồng).

a) Biết có 1 trong 10 ngày trên có sự bất thường trong giá cổ phiếu. Hãy tìm ngày đó và giải thích.

b) Sau khi bỏ đi ngày có giá bất thường, hãy cho biết giá cổ phiếu nào ổn định hơn. Tại sao?

Lời giải:

a) +) Mã cổ phiếu A:

Áp dụng các bước tìm tứ phân vị ta tìm được Q₁ = 45,1, Q₃ = 45,5

Khi đó khoảng tứ phân vị là ∆_Q = Q₃ − Q₁ = 45,5 – 45,1 = 0,4.

Giá trị ngoại lệ x thỏa mãn

x > Q₃ + 1,5∆_Q = 45,5 + 1,5.0,4 = 46,1

Hoặc x < Q₁ − 1,5∆_Q = 45,1 − 1,5.0,4 = 44,5

Vậy đối chiếu mẫu số liệu của A suy ra giá trị ngoại lệ là 35,5 và rơi vào ngày thứ 4.

+) Mã cổ phiếu B:

Áp dụng các bước tìm tứ phân vị ta dễ dàng tìm được Q₁ = 47,8, Q₃ = 49

Khi đó khoảng tứ phân vị là ∆_Q = Q₃ − Q₁ = 49 – 47,8 = 1,2.

Giá trị ngoại lệ x thỏa mãn

x > Q₃ + 1,5∆_Q = 49 + 1,5.1,2 = 50,8

Hoặc x < Q₁ − 1,5∆_Q = 47,8 − 1,5.1,2 = 46

Vậy đối chiếu mẫu số liệu của B suy ra giá trị ngoại lệ là 68,4 và rơi vào ngày thứ 4.

b) Sau khi bỏ đi giá trị ngoại lệ thì giá trị trung bình của mẫu của A là:

Khi đó phương sai của mẫu số liệu của A là

Và giá trị trung bình của mẫu của B là:

Khi đó phương sai của mẫu số liệu của B là

Vậy so sánh hai phương sai mẫu ta thấy 0,036 < 0,505 nên giá của mã cổ phiếu A ổn định hơn giá của mã cổ phiếu B.