Sách bài tập Toán 10 trang 100 Chân trời sáng tạo

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 10 trang 100 trong Bài 4: Tích vô hướng của hai vectơ. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải SBT Toán 10 trang 100 Tập 1 Chân trời sáng tạo

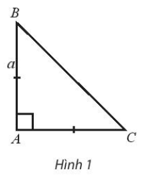
Bài 1 trang 100 SBT Toán 10 Tập 1: Cho tam giác vuông cân ABC có AB = AC = a.

Tính các tích vô hướng $\overrightarrow{\mathrm{AB}}.\overrightarrow{\text{AC}}$, $\overrightarrow{\text{AC}}.\overrightarrow{\text{CB}}$.

Lời giải:

Do tam giác ABC vuông tại A nên AB ⊥AC⇒ $\overrightarrow{\mathrm{AB}}.\overrightarrow{\text{AC}}$ = 0;

Ta có: CB = $\sqrt{{\text{AB}}^2+{\text{AC}}^2}$ = $\sqrt{{\text{a}}^2+{\text{a}}^2}$ = a$\sqrt{2}$

Tam giác ABC vuông cân tại A nên $\widehat{\text{ACB}}$ = 45°

Như vậy: $\overrightarrow{\text{AC}}.\overrightarrow{\text{CB}}$ = $-\overrightarrow{\text{CA}}.\overrightarrow{\text{CB}}$ = $-(\overrightarrow{\text{CA}}.\overrightarrow{\text{CB}})$ = $-\overrightarrow{\left(\text{CA}\right)}.\overrightarrow{\left(\text{CB}\right)}.\cos 45°$ = – a. a$\sqrt{2}$.$\frac{\sqrt{2}}{2}$ = –a²

Vậy $\overrightarrow{\mathrm{AB}}.\overrightarrow{\text{AC}}$ = 0 và $\overrightarrow{\text{AC}}.\overrightarrow{\text{CB}}$ = –a².

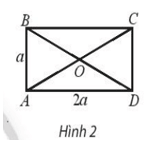
Bài 2 trang 100 SBT Toán 10 Tập 1: Cho hình chữ nhật ABCD có tâm O và AD = 2a, AB = a. Tính:

a) $\overrightarrow{\text{AB}}.\overrightarrow{\text{AO}}$;

b) $\overrightarrow{\text{AB}}.\overrightarrow{\text{AD}}\text{}$.

Lời giải:

a) Vì ABCD là hình chữ nhật nên AB = CD = a, AD = BC = 2a.

Ta có: AC = $\sqrt{{\text{AB}}^2+{\text{BC}}^2}$ = $\sqrt{{\text{a}}^2+{\left(2\text{a}\right)}^2}$ = a$\sqrt{5}$.

Xét tam giác BAC vuông tại B, có: cos$\widehat{\mathrm{BAO}}$ = cos$\widehat{\text{BAC}}$= $\frac{\text{AB}}{\text{AC}}=\frac{a}{\sqrt{5}a}=\frac{1}{\sqrt{5}}$.

ABCD là hình chữ nhật nên O là trung điểm của AC và BD

⇒ AO = $\frac{1}{2}$AC = $\frac{\text{a}\sqrt{5}}{2}$.

$\overrightarrow{\text{AB}}.\overrightarrow{\text{AO}}$ = $\overrightarrow{\left(\text{AB}\right)}$. $\overrightarrow{\left(\text{AO}\right)}$. cos$\widehat{\mathrm{BAO}}$ = a. $\frac{\text{a}\sqrt{5}}{2}$. $\frac{1}{\sqrt{5}}$ = $\frac{{\text{a}}^2}{2}$.

Vậy $\overrightarrow{\text{AB}}.\overrightarrow{\text{AO}}$ = $\frac{{\text{a}}^2}{2}$.

b) Do ABCD là hình chữ nhật nên $\overrightarrow{\text{AB}}$ ⊥ $\overrightarrow{\text{AD}}$ ⇒ $\overrightarrow{\mathrm{AB}}.\overrightarrow{\text{AD}}$ = 0.