Sách bài tập Toán 10 trang 45 Chân trời sáng tạo

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 10 trang 45 trong Bài 1: Hàm số và đồ thị. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

• Bài 1 trang 45 SBT Toán lớp 10 Tập 1
• Bài 2 trang 45 SBT Toán lớp 10 Tập 1

Giải SBT Toán 10 trang 45 Tập 1 Chân trời sáng tạo

Bài 1 trang 45 SBT Toán 10 Tập 1: Tập xác định của các hàm số sau:

a) f(x) = $\frac{4x-1}{\sqrt{2x-5}}$ ;

b) f(x) = $\frac{2-x}{\left(x+3\right)\left(x-7\right)}$ ;

c)

$f\left(x\right)=\left(\begin{array}{c}\frac{1}{x-3}khix\ge 0\\ 1khix<0\end{array}\right)$ .

Lời giải:

a) Biểu thức có nghĩa khi 2x – 5 > 0 hay x > . $\frac{5}{2}$

Vậy tập xác định của hàm số là D = $\left(\frac{5}{2};+\infty \right)$ .

b) Biểu thức $\frac{2-x}{\left(x+3\right)\left(x-7\right)}$ có nghĩa khi (x + 3)(x – 7) ≠ 0 ⇒ x ≠ – 3 và x ≠ 7.

Vậy tập xác định của hàm số là D = ℝ \ {– 3; 7}.

c) Hàm số lấy giá trị bằng 1 khi x < 0 nên hàm số xác định với mọi x < 0.

Khi x ≥ 0, hàm số xác định khi và chỉ khi x – 3 ≠ 0 ⇒ x ≠ 3.

Vậy tập xác định của hàm số là D = ℝ \ {3}.

Bài 2 trang 45 SBT Toán 10 Tập 1: Vẽ đồ thị các hàm số sau:

a)

$f\left(x\right)=\left(\begin{array}{c}{x}^{2}khix\le 2\\ x+2khix>2;\end{array}\right)$

b) f(x) = |x + 3| – 2.

Lời giải:

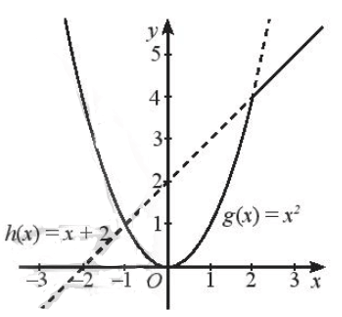
a) + Vẽ đồ thị hàm số g(x) = x² và giữ lại phần đồ thị ứng với x ≤ 2:

Đồ thị hàm số g(x) = x² là một parabol có đỉnh là gốc tọa độ O, trục đối xứng là trục Oy, đồ thị có bề lõm hướng lên trên, đi qua các điểm (1; 1), (– 1; 1), (2; 4), (– 2; 4).

Ta giữ lại phần đồ thị nằm bên trái đường thẳng x = 2:

+ Vẽ đồ thị hàm số h(x) = x + 2 và giữ lại phần đồ thị ứng với x > 2.

Đồ thị hàm số h(x) = x + 2 là một đường thẳng đi qua hai điểm (0; 2) và (– 2; 0).

Ta giữ lại phần đường thẳng nằm bên phải đường thẳng x = 2.

Ta được đồ thị cần vẽ như hình sau:



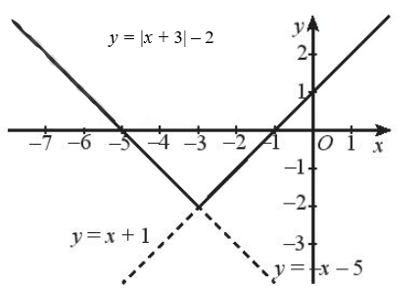
b) Với x + 3 ≥ 0 ⇔ x ≥ – 3, ta có: |x + 3| – 2 = x + 3 – 2 = x + 1.

Với x + 3 < 0 ⇔ x < – 3, ta có: |x + 3| – 2 = – (x + 3) – 2 = – x – 3 – 2 = – x – 5.

Khi đó ta có:

$f\left(x\right)=\left(\begin{array}{c}x+1khix\ge -3\\ -x-5khix<-3\end{array}\right)$ .

Ta vẽ đồ thị hàm số g(x) = x + 1 và giữ lại phần đồ thị ứng với x ≥ – 3: Đồ thị hàm số g(x) = x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; 0).

Ta vẽ đồ thị hàm số h(x) = – x – 5 và giữ lại phần đồ thị ứng với x < – 3: Đồ thị hàm số h(x) = – x – 5 là đường thẳng đi qua hai điểm (– 5; 0) và (– 3; – 2).

Ta được đồ thị của hàm số cần vẽ như hình sau: