Sách bài tập Toán 10 trang 57 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 10 trang 57 trong Bài tập cuối chương 3. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải SBT Toán 10 trang 57 Tập 1 Chân trời sáng tạo

Bài 5 trang 57 SBT Toán 10 Tập 1: Tập giá trị của hàm số y = f(x) = – 2x² + $\sqrt{2}$x + 1 là

A. T = $\left(-\frac{5}{4};+\infty \right)$;

B. T = $\left(-\frac{5}{4};+\infty \right)$;

C. T = $\left(-\infty ;\frac{5}{4}\right)$;

D. T = $\left(-\infty ;\frac{5}{4}\right)$.

Lời giải:

Đáp án đúng là: D

Do hàm số y = f(x) = – 2x² + $\sqrt{2}$x + 1 là hàm số bậc hai nên đồ thị hàm số này là parabol có tọa độ đỉnh S là

x_S = $-\frac{b}{2a}$ $=-\frac{\sqrt{2}}{2.\left(-2\right)}$ = $\frac{\sqrt{2}}{4}$,

y_S = $-2.{\left(\frac{\sqrt{2}}{4}\right)}^2+\sqrt{2}.\frac{\sqrt{2}}{4}+1=\frac{5}{4}$ hay S $\left(\frac{\sqrt{2}}{4};\frac{5}{4}\right)$.

Lại có hàm số có hệ số a = – 2 < 0 nên bề lõm của parabol hướng xuống dưới, do đó đỉnh S là điểm cao nhất của đồ thị hàm số.

Vậy tập giá trị của hàm số đã cho là: T = $\left(-\infty ;\frac{5}{4}\right)$.

Bài 6 trang 57 SBT Toán 10 Tập 1: Hàm số y = f(x) = –(x + 2)(x – 4) đồng biến trên khoảng:

A. (– ∞; – 1);

B. (1; + ∞);

C. (– ∞; 1);

D. (– 1; + ∞).

Lời giải:

Đáp án đúng là: C

Ta có: – (x + 2)(x – 4) = – x² + 4x – 2x + 8 = – x² + 2x + 8.

Do đó ta có hàm số y = f(x) = – x² + 2x + 8.

Đây là hàm số bậc hai nên đồ thị hàm số là parabol với tọa độ đỉnh S là

x_S = $-\frac{b}{2a}=-\frac{2}{2.\left(-1\right)}=1$,

y_S = – 1² + 2 . 1 + 8 = 9 hay S(1; 9).

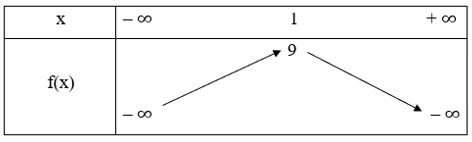
Do hệ số a = – 1 < 0 nên ta có bảng biến thiên:

Vậy hàm số đã cho đồng biến trên khoảng (– ∞; 1).

Bài 7 trang 57 SBT Toán 10 Tập 1: Hàm số y = f(x) = (x + 2)(x – 2) có:

A. Giá trị nhỏ nhất là 4;

B. Giá trị lớn nhất là 4;

C. Giá trị lớn nhất là – 4;

D. Giá trị nhỏ nhất là – 4.

Lời giải:

Đáp án đúng là: D

Ta có: (x + 2)(x – 2) = x² – 4.

Do đó ta có hàm số y = f(x) = x² – 4 là hàm số bậc hai có đồ thị là một parabol với tọa độ đỉnh S là $x_S=-\frac{b}{2a}=-\frac{0}{2.1}=0$, y_S = 0² – 4 = – 4 hay S(0; – 4).

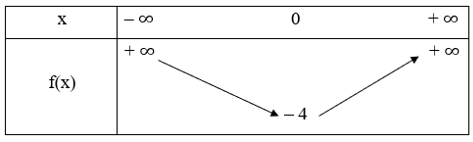
Vì hệ số a = 1 > 0 nên ta có bảng biến thiên

Từ bảng biến thiên, ta có giá trị nhỏ nhất của hàm số là – 4.

Bài 8 trang 57 SBT Toán 10 Tập 1: Để hàm số y = f(x) = (m – 2)(x + 5)² + (m² – 4) |x – 7| + 3 là một hàm số bậc hai thì giá trị của m là:

A. 2;

B. 2 hay – 2;

C. – 2;

D. 4.

Lời giải:

Đáp án đúng là: C

Ta có: y = f(x) = (m – 2)(x + 5)² + (m² – 4)|x – 7| + 3

⇔ y = f(x) = (m – 2)x² + 10(m – 2)x + 25(m – 2) + (m² – 4)|x – 7| + 3

Hàm số bậc hai có dạng y = ax² + bx + c với a ≠ 0 và không chứa dấu giá trị tuyệt đối.

Do đó, hàm số đã cho là hàm số bậc hai khi và chỉ khi $\left(\begin{array}{c}m-2\ne 0\\ m^2-4=0\end{array}\right)$

$\iff \left(\begin{array}{c}m\ne 2\\ m=\pm 2\end{array}\right)$⇔ m = – 2.

Vậy m = – 2 thì thỏa mãn.

Bài 9 trang 57 SBT Toán 10 Tập 1: Đồ thị hàm số y = f(x) = –x² + 4(5m + 1)x + (3 – 2m) có trục đối xứng là đường thẳng x = – 2 khi m có giá trị là:

A. – 3;

B. $-\frac{2}{5}$;

C. $\frac{3}{2}$;

D. $-\frac{1}{5}$.

Lời giải:

Đáp án đúng là: B

Hàm số y = f(x) = –x² + 4(5m + 1)x + (3 – 2m) là hàm số bậc hai.

Đồ thị hàm số này có trục đối xứng là đường thẳng x = – 2 khi và chỉ khi $-\frac{b}{2a}=–2$.

Suy ra b = 4a hay 4(5m + 1) = 4 . (– 1) ⇔ 20m + 4 = – 4 ⇔ 20m = – 8 ⇔ m = $-\frac{2}{5}$.

Vậy m = $-\frac{2}{5}$ thì thỏa mãn yêu cầu bài toán.

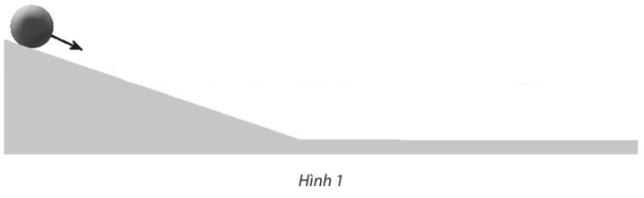
Bài 10 trang 57 SBT Toán 10 Tập 1: Một viên bi được thả không vận tốc đầu và lăn trên máng nghiêng như Hình 1.

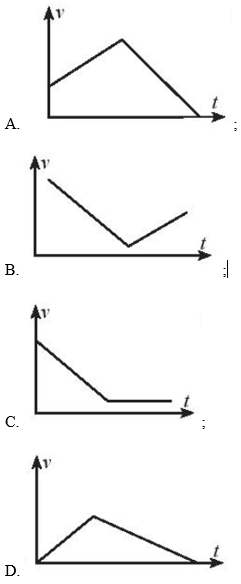
Đồ thị nào sau đây phù hợp với sự thay đổi vận tốc của viên bi theo thời gian?

Lời giải:

Đáp án đúng là: C

Quan sát Hình 1, ta thấy viên bi rơi từ trên cao xuống theo mặt phẳng nghiêng và tiếp tục lăn trên mặt phẳng ngang theo một đường thẳng. Do đó, trong các đồ thị ở trên, đồ thị ở đáp án C là phù hợp với sự thay đổi vận tốc của viên bi theo thời gian.