Sách bài tập Toán 10 trang 69 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 10 trang 69 trong Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải SBT Toán 10 trang 69 Tập 1 Chân trời sáng tạo

Bài 1 trang 69 SBT Toán 10 Tập 1: Tính giá trị của T = 4cos60° + 2sin135° + 3cot120°.

Lời giải:

Sử dụng máy tính cầm tay ta có:

T = 4cos60° + 2sin135° + 3cot120°

T = 4.$\frac{1}{2}$ + 2.$\frac{\sqrt{2}}{2}$ + 3.$\frac{-1}{\sqrt{3}}$

T = 2 + $\sqrt{2}$ – $\sqrt{3}$

Vậy T = 2 + $\sqrt{2}$ – $\sqrt{3}$.

Bài 2 trang 69 SBT Toán 10 Tập 1: Chứng minh rằng:

a) sin138° = sin42°;

b) tan125° = – cot35°.

Lời giải:

a) Ta có sinx = sin(180° – x ) nên:

sin138° = sin (180° – 138°) = sin42°.

Vậy sin138° = sin42°.

b) Ta có tanx = –tan(180° – x) và tanx = cot( 90° – x )

tan125 = –tan(180° – 125°) = –tan55° = –cot( 90° – 55° ) = –cot35°.

Vậy tan125° = – cot35°.

Bài 3 trang 69 SBT Toán 10 Tập 1: Tìm góc α ( 0° ≤ α ≤ 180° ) trong mỗi trường hợp sau:

a) cos α = $-\frac{\sqrt{3}}{2}$;

b) sin α = $\frac{\sqrt{3}}{2}$;

c) tan α = $-\frac{\sqrt{3}}{3}$;

d) cot α = –1.

Lời giải:

a) Sử dụng máy tính cầm tay, ta có được: α = 150°.

b) Sử dụng máy tính cầm tay, ta có được: α = 60°.

Lại có sinα = sin(180° – α ) nên α = 120°.

Vậy α = 60° hoặc α = 120°.

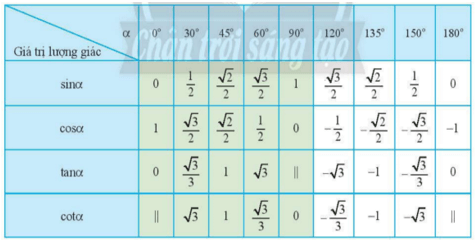
c) Dựa vào bảng các giá trị lượng giác đặc biệt, ta có: tan α = $-\frac{\sqrt{3}}{3}$⇒ α = 150°.

d) Dựa vào bảng các giá trị lượng giác đặc biệt, ta có: cot α = –1 ⇒ α = 135°.

Vậy α = 135°.

Bài 4 trang 69 SBT Toán 10 Tập 1: Chứng minh rằng trong tam giác ABC ta có:

a) tanB = –tan( A+C);

b) sinC = sin ( A+B ).

Lời giải:

a) Trong tam giác ABC có: $\hat{\text{A}}$ + $\hat{\text{B}}$ + $\hat{\text{C}}$ = 180° ⇒ $\hat{\text{A}}$ + $\hat{\text{C}}$= 180° – $\hat{\text{B}}$

Ta có: tanα = –tan(180° – α ) nên

tanB = –tan( 180° – B ) = –tan( A+C)

Vậy tanB = –tan( A+C).

b) Trong tam giác ABC có: $\hat{\text{A}}$ + $\hat{\text{B}}$ + $\hat{\text{C}}$ = 180° ⇒ $\hat{\text{A}}$ +$\hat{\text{C}}$ = 180° – $\hat{\text{B}}$.

Ta có: sinα = sin(180° – α ) nên

sinC = sin(180° – C ) = sin ( A+B ).

Vậy sinC = sin ( A+B ).

Bài 5 trang 69 SBT Toán 10 Tập 1: Chứng minh rằng với mọi góc x ( 0° ≤ x ≤ 90°), ta đều có:

a) sinx = $\sqrt{1-{\cos }^2\text{x}}$;

b) cosx = $\sqrt{1-{\sin }^2\text{x}}$;

c) tan²x = $\frac{{\sin }^2\text{x}}{{\cos }^2\text{x}}$ ( x ≠ 90°); d) cot²x = $\frac{{\cos }^2\text{x}}{{\sin }^2\text{x}}$ ( x ≠ 0°).

Lời giải:

a) Ta có: ${\text{cos}}^{\text{2}}{\text{x + sin}}^{\text{2}}\text{x=1}$.

⇒ sin²x = 1 – cos²x

⇒ sinx = $\sqrt{1-{\cos }^2\text{x}}$ hoặc sinx = $-\sqrt{1-{\cos }^2\text{x}}$

Vì 0° ≤ x ≤ 90° nên 0 ≤ sinx ≤ 1. Do đó chỉ có sinx = $\sqrt{1-{\cos }^2\text{x}}$ là thỏa mãn.

Vậy sinx = $\sqrt{1-{\cos }^2\text{x}}$.

b) Ta có: cos²x + sin²x = 1

⇒ cos²x = 1 – sin²x.

⇒ cosx = $\sqrt{1-{\sin }^2\text{x}}$ hoặc cosx = $-\sqrt{1-{\sin }^2\text{x}}$

Vì 0° ≤ x ≤ 90° nên 0 ≤ cos ≤ 1. Do đó chỉ có cosx = $\sqrt{1-{\sin }^2\text{x}}$ là thỏa mãn.

Vậy cosx = $\sqrt{1-{\sin }^2\text{x}}$.

c) Ta có: tanx = $\frac{\sin \text{x}}{\cos \text{x}}$ ⇒ tan²x = $\frac{{\sin }^2\text{x}}{{\cos }^2\text{x}}$( x ≠ 90°). (ĐPCM)

d) Ta có: cotx = $\frac{\cos \text{x}}{\sin \text{x}}$ ⇒ cot²x = $\frac{{\cos }^2\text{x}}{{\sin }^2\text{x}}$ ( x ≠ 0°). (ĐPCM)

Bài 6 trang 69 SBT Toán 10 Tập 1: Cho góc x với cosx = $\frac{-1}{2}$. Tính giá trị biểu thức

S = 4sin²x + 8tan²x.

Lời giải:

Sử dụng máy tính cầm tay, ta có: cosx = $\frac{-1}{2}$ ⇒ x = 120° ⇒ sinx = $\frac{\sqrt{3}}{2}$ và tanx = $-\sqrt{3}$.

S = 4sin²x + 8tan²x = 4. ${\left(\frac{\sqrt{3}}{2}\right)}^2$+ 8. ${(-\sqrt{3})}^2$ = 4.$\frac{3}{4}$ + 8.3 = 27.

Vậy S = 27.

Bài 7 trang 69 SBT Toán 10 Tập 1: Dùng máy tính cầm tay, tính.

a) sin138°12’24’’;

b) cos144°35’12’’;

c) tan152°35’44’’.

Lời giải:

Sử dụng máy tính cầm tay, ta tính được:

a) sin138°12’24’’ ≈ 0,666.

b) cos144°35’12’’≈ –0,815.

c) tan152°35’44’’ ≈ –0,518.

Bài 8 trang 69 SBT Toán 10 Tập 1: Dùng máy tính cầm tay, tìm x, biết:

a) cosx = –0,234;

b) sinx = 0,812;

c) cotx = –0,333.

Lời giải:

Sử dụng máy tính cầm tay, ta tính được:

a) cosx = –0,234 ⇒ x ≈ 103°31’58’’.

b) sinx = 0,812 ⇒ x ≈ 54°17’30’’ hay x ≈ 125°42’30’’.

c) cotx = –0,333 ⇒ x ≈ 108°25’4’’.