Sách bài tập Toán 10 trang 74 Chân trời sáng tạo

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 10 trang 74 trong Bài 2: Định lí côsin và định lí sin. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải SBT Toán 10 trang 74 Tập 1 Chân trời sáng tạo

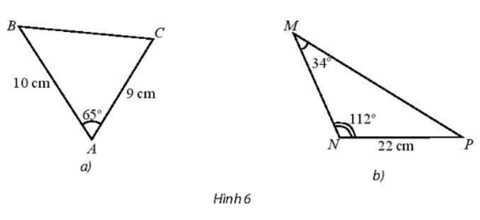
Bài 1 trang 74 SBT Toán 10 Tập 1: Tính độ dài các cạnh chưa biết trong tam giác sau:

Lời giải:

a) Áp dụng định lí côsin ta có:

BC² = AB² + AC² – 2.AB.AC.cos$\hat{\text{A}}$

BC² = 10² + 9² – 2.10.9.cos65°

BC ² ≈ 104,929

BC ≈ 10,24 (cm).

Vậy BC ≈ 10,24 (cm).

b) $\hat{\text{P}}$ = 180° – 112° – 34° = 34°.

Ta có: $\hat{\text{P}}$ = $\hat{\text{M}}$ ⇒ tam giác MNP cân tại N ⇒ MN = NP = 22 (cm)

Áp dụng định lí sin ta có:

$\frac{\text{MP}}{\text{sinN}}\text{=}\frac{\text{MN}}{\text{sinP}}\text{=}\frac{\text{NP}}{\text{sinM}}=\frac{22}{\sin 34°}$.

⇒ MP = $\frac{22}{\sin 34°}$.sin112° ≈ 36,48 (cm)

Vậy MP ≈ 36,48 cm, MN = 22 cm.

Bài 2 trang 74 SBT Toán 10 Tập 1: Cho tam giác ABC biết cạnh a = 75 cm, $\hat{\text{B}}$ = 80°, $\hat{\text{C}}$ = 40°.

a) Tính các góc, các cạnh còn lại của tam giác ABC.

b) Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Lời giải:

a) Ta có: $\hat{\text{A}}$ = 180° – 80° – 40° = 60°.

Áp dụng định lí sin ta có:

$\frac{\text{a}}{\text{sinA}}\text{=}\frac{\text{b}}{\text{sinB}}\text{=}\frac{\text{c}}{\text{sinC}}$ = $\frac{75}{\sin 60°}$

⇒ b = $\frac{75}{\sin 60°}$. sin80° ≈ 85,29 (cm);

⇒ c = $\frac{75}{\sin 60°}$. sin40° ≈ 55,67 (cm).

Vậy AC ≈ 85,29 cm; AB ≈ 55,67 cm và $\hat{\text{A}}$= 60°.

b) R = $\frac{\text{a}}{\text{2sinA}}$ = $\frac{75}{2.\sin 60°}$ = 25$\sqrt{3}$ (cm).

Vậy R = 25$\sqrt{3}$ cm.