Sách bài tập Toán 10 trang 80 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 10 trang 80 trong Bài tập cuối chương 4. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải SBT Toán 10 trang 80 Tập 1 Chân trời sáng tạo

Bài 1 trang 80 SBT Toán 10 Tập 1: Khẳng định nào sau đây là đúng?

A. sinα = sin( 180° – α );

B. cosα = cos( 180° – α );

C. tanα = tan( 180° – α );

D. cotα = cot( 180° – α );

Lời giải:

Đáp án đúng là A

Ta có sin của hai góc bù nhau thì bằng nhau. Côsin, tan và côtan của hai góc bù nhau thì đối nhau. Vậy khẳng định đúng là A.

Bài 2 trang 80 SBT Toán 10 Tập 1: Trong các khẳng định sau đây, khẳng định nào sai?

A. cos45° = sin45°;

B. cos45° = sin135°;

C. cos30° = sin120°;

D. sin60° = cos120°.

Lời giải:

Đáp án đúng là D

cos45° = sin( 90° – 45° ) = sin45°. Khẳng định A đúng.

cos45° = sin( 90° – 45° ) = sin45° = sin ( 180° – 45° ) = sin135°. Khẳng định B đúng.

cos30° = sin ( 90° – 30° ) = sin60° = sin ( 180° – 60° ) = sin120°. Khẳng định C đúng.

Có sin60° = cos30° ≠ cos120°. Khẳng định D sai.

Vậy chọn đáp án D.

Bài 3 trang 80 SBT Toán 10 Tập 1: Bất đẳng thức nào dưới đây là đúng?

A. sin90° < sin150°;

B. sin90°15’ < sin90°30’;

C. cos90°30’ > cos100°;

D. cos150° > cos120°.

Lời giải:

Đáp án đúng là C

Ta có:

sin90° = 1 mà sin150° = $\frac{1}{2}$ ⇒ sin90° > sin150°. Vì vậy A sai.

sin90°15’ = 0,99999, sin90°30’ = 0,99996 ⇒ sin90°15’ > sin90°30’. Vì vậy B sai.

cos90°30’ ≈ – 8,72. 10^-3 , cos100° ≈ – 0,17 ⇒ cos90°30’ > cos100°. Vì vậy C đúng.

cos150° = $\frac{-\sqrt{3}}{2}$, cos120° = $\frac{-1}{2}$ ⇒ cos150° < cos120°. Vì vậy D sai.

Chọn đáp án C.

Bài 4 trang 80 SBT Toán 10 Tập 1: Trong các đẳng thức sau đây, đẳng thức nào là đúng?

A. sin150° = $\frac{-\sqrt{3}}{2}$;

B. cos150° = $\frac{\sqrt{3}}{2}$;

C. tan150° = $\frac{-1}{\sqrt{3}}$;

D. cot150° = $\sqrt{3}$.

Lời giải:

Đáp án đúng là C

Sử dụng máy tính cầm tay ta tính được

sin150° = $\frac{1}{2}$, cos150° = $\frac{-\sqrt{3}}{2}$, tan150° = $\frac{-1}{\sqrt{3}}$, cot150° = $-\sqrt{3}$.

Vậy khẳng định C đúng.

Bài 5 trang 80 SBT Toán 10 Tập 1: Cho tam giác ABC có BC = a, AC = b, AB = c. Mệnh đề nào sau đây đúng?

A. Nếu b² + c² – a² > 0 thì góc A nhọn;

B. Nếu b² + c² – a² > 0 thì góc A tù;

C. Nếu b² + c² – a² < 0 thì góc A nhọn;

D. Nếu b² + c² – a² < 0 thì góc A vuông.

Lời giải:

Đáp án đúng là A

Theo định lí côsin ta có: a² = b² + c² – 2bccosA

Nếu b² + c² – a² > 0 hay b² + c² > a² thì 2bccosA > 0 hay cosA > 0 ( b,c là cạnh tam giác nên b,c > 0 ). Khi đó $\hat{\text{A}}$ < 90° hay góc A nhọn.

Nếu b² + c² – a² < 0 hay b² + c² < a² thì 2bccosA < 0 hay cosA < 0 ( b,c là cạnh tam giác nên b,c > 0 ). Khi đó $\hat{\text{A}}$ > 90° hay góc A tù.

Như vậy đáp án đúng là A.

Bài 6 trang 80 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 4 cm, BC = 7 cm, CA = 9 cm. Giá trị cosA là:

A. $\frac{2}{3}$;

B. $\frac{1}{3}$;

C. $\frac{-2}{3}$;

D. $\frac{1}{2}$.

Lời giải:

Đáp án đúng là A

Áp dụng hệ quả định lí côsin ta có:

cosA = $\frac{{\mathrm{AC}}^2+{\text{AB}}^2-{\text{BC}}^2}{2\text{AB.AC}}$ = $\frac{4^2+9^2-7^2}{\mathrm{2.4.9}}$ = $\frac{2}{3}$.

Vậy chọn đáp án A.

Bài 7 trang 80 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 8 cm, AC = 18 cm và có diện tích bằng 64cm². Giá trị sinA là:

A. $\frac{\sqrt{3}}{2}$;

B. $\frac{3}{8}$;

C. $\frac{4}{5}$;

D. $\frac{8}{9}$.

Lời giải:

Đáp án đúng là D

Ta có: S = $\frac{1}{2}$AB.AC. sinA ⇒ sinA = $\frac{2\text{S}}{\text{AB.AC}}$ = $\frac{64.2}{18.8}=\frac{8}{9}$.

Vậy đáp án đúng là D.

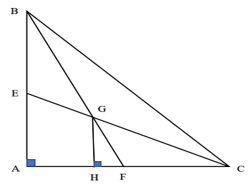
Bài 8 trang 80 SBT Toán 10 Tập 1: Cho tam giác ABC vuông cân tại A có AB = AC = 30 cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC là:

A. 50 cm²;

B. 50$\sqrt{2}$ cm²;

C. 75 cm²;

D. 15$\sqrt{105}$ cm².

Lời giải:

Đáp án đúng là C

Kẻ GH vuông góc với AC.

G là trọng tâm tam giác ABC ⇒ GF = $\frac{1}{3}$BF .

Xét tam giác GFH và tam giác BFA:

$\widehat{\text{GHF}}=\widehat{\text{BAF}}$ = 90°

$\widehat{\text{GFH}}=\widehat{\text{BFA}}$ (hay chung $\widehat{GFH}$)

⇒ tam giác GFH và tam giác BFA đồng dạng (g.g)

⇒ $\frac{\text{GH}}{\text{AB}}\text{=}\frac{\text{GF}}{\text{BF}}\text{=}\frac{\text{1}}{\text{3}}$ ( Tính chất hai tam giác đồng dạng)

⇒ GH = 10 cm

Lại có FC = $\frac{1}{2}$AC = 15 cm

⇒ S_GFC = 10.15. $\frac{1}{2}$ = 75 cm²

Vậy đáp án C đúng.