Giải SBT Toán 10 trang 31 Tập 2 Kết nối tri thức

---

Với Giải SBT Toán 10 trang 31 Tập 2 trong Bài 19: Phương trình đường thẳng Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 31.

Giải SBT Toán 10 trang 31 Tập 2 Kết nối tri thức

Bài 7.1 trang 31 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho điểm D(0; 2) và hai vectơ $\overrightarrow{n}=(1;-3),\overrightarrow{u}=(1;3)$.

a) Viết phương trình tổng quát của đường thẳng d đi qua D và nhận $\overrightarrow{n}$ là một vectơ pháp tuyến.

b) Viết phương trình tham số của đường thẳng Δ đi qua D và nhận $\overrightarrow{u}$ là một vectơ chỉ phương.

Hướng dẫn giải:

a)

Phương trình tổng quát của đường thẳng d đi qua D và nhận là một vectơ pháp tuyến là:

1(x – 0) – 3(y – 2) = 0

⇔ x – 3y + 6 = 0

Vậy d: x – 3y + 6 = 0.

b)

Phương trình tham số của đường thẳng ∆ đi qua D và nhận là một vectơ chỉ phương là:

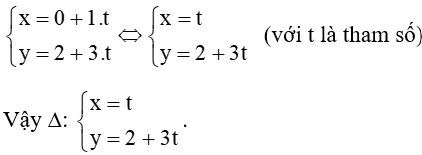
Bài 7.2 trang 31 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho ba điểm A(1; 2), B(0; –1) và C(–2; 3). Lập phương trình tổng quát của đường thẳng qua A và vuông góc với đường thẳng BC.

Hướng dẫn giải:

Đường thẳng d qua A và vuông góc với đường thẳng BC nhận vectơ $\overrightarrow{BC}$ làm vectơ pháp tuyến.

$\overrightarrow{BC}$ = (–2 – 0; 3 + 1) = (–2; 4)

Phương trình của đường thẳng d là:

–2(x – 1) + 4(y – 2) = 0

⇔ –2x + 2 + 4y – 8 = 0

⇔ –2x + 4y – 6 = 0

⇔ x – 2y + 3 = 0

Vậy d: x – 2y + 3 = 0.

Bài 7.3 trang 31 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(2; 3). Tìm một vectơ chỉ phương của đường thẳng AB và viết phương trình tham số của đường thẳng AB.

Hướng dẫn giải:

Một vectơ chỉ phương của đường thẳng AB chính là vectơ $\overrightarrow{AB}$.

Ta có: $\overrightarrow{AB}$ = (1; 1)

Đường thẳng AB đi qua điểm A(1; 2) có vectơ chỉ phương $\overrightarrow{AB}$ = (1; 1) có phương trình tham số là:

Bài 7.4 trang 31 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng ∆: 2x – y + 5 = 0. Tìm tất cả các vectơ pháp tuyến có độ dài $2\sqrt{5}$ của đường thẳng ∆.

Hướng dẫn giải:

Dựa vào phương trình tổng quát của đường thẳng ∆: 2x – y + 5 = 0. Đường thẳng ∆ có một vectơ pháp tuyến là $\overrightarrow{n}=(2;-1)$ nên các vectơ pháp tuyến của ∆ có dạng là $\overrightarrow{n\text{'}}=(2t;-t)$. Theo giả thiết ta có:

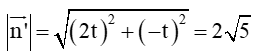
⇔ 4t² + t² = 20

⇔ 5t² = 20

⇔ t² = 4

⇔ t = ±2

Với t = 2, ta được vectơ pháp tuyến thỏa mãn yêu cầu đề bài là: $\overrightarrow{n_1\text{'}}$ = (4; –2)

Với t = – 2, ta được vectơ pháp tuyến thỏa mãn yêu cầu đề bài là: $\overrightarrow{n_2\text{'}}$ = (–4; 2).

Vậy có hai vectơ pháp tuyến thỏa mãn là $\overrightarrow{n_1\text{'}}$ = (4; –2) và $\overrightarrow{n_2\text{'}}$ = (–4; 2).

Bài 7.5 trang 31 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng d có phương trình y = –2x + 3. Viết phương trình tham số và phương trình tổng quát của đường thẳng d.

Hướng dẫn giải:

Ta có: y = –2x + 3 ⇔ 2x + y – 3 = 0

Phương trình tổng quát của đường thẳng d là: 2x + y – 3 = 0.

Từ phương trình tổng quát ta thấy đường thẳng d: 2x + y – 3 = 0 có một vectơ pháp tuyến là: $\overrightarrow{n}$ = (2; 1), do đó, nó có một vectơ chỉ phương là $\overrightarrow{u}$ = (1; –2).

Thay x = 1 vào phương trình tổng quát ta có: y = 1.

Chọn điểm (1; 1) thuộc đường thẳng d: 2x + y – 3 = 0. Phương trình tham số của đường thẳng này là:

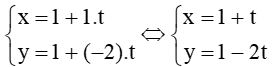
Bài 7.6 trang 31 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho điểm M(2; 1) và đường thẳng 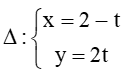. Tìm điểm N thuộc đường thẳng ∆ sao cho $MN=\sqrt{2}$.

Hướng dẫn giải:

Do N thuộc đường thẳng ∆ nên tọa độ của N có dạng: (2 – t; 2t).

Ta có: $\overrightarrow{MN}$ = (2 – t – 2; 2t – 1) = (–t; 2t – 1)

$MN=\sqrt{2}$

$\iff \sqrt{{(-t)}^2+{(2t-1)}^2}=\sqrt{2}$

⇔ (– t)² + (2t – 1)² = 2

⇔ t² + 4t² – 4t + 1 = 2

⇔ 5t² – 4t – 1 = 0

⇔ t = 1 hoặc t = $-\frac{1}{5}$

Với t = 1, ta có N(1; 2)

Với t = $-\frac{1}{5}$, ta có $N\left(\frac{11}{5};-\frac{2}{5}\right)$.

Vậy có hai điểm N thỏa mãn là N(1; 2) và $N\left(\frac{11}{5};-\frac{2}{5}\right)$.

Bài 7.7 trang 31 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho tam giác ABC có toạ độ ba đỉnh A(0; –1), B(2; 3) và C(–4; 1). Lập phương trình tham số của đường trung bình ứng với cạnh BC của tam giác ABC.

Hướng dẫn giải:

Gọi d là đường trung bình ứng với cạnh BC của tam giác ABC nên d // BC và d đi qua trung điểm M của AB, do đó:

Đường thẳng d nhận vectơ $\overrightarrow{BC}$ = (–4 – 2; 1 – 3) = (–6; –2) là một vectơ chỉ phương.

Tọa độ trung điểm M là x_M = $\frac{0+2}{2}=1$; y_M = $\frac{(-1)+3}{2}=1$.

Suy ra M(1; 1) thuộc d.

Phương trình tham số của d là:

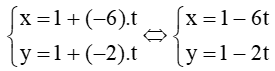
Lời giải sách bài tập Toán lớp 10 Bài 19: Phương trình đường thẳng Kết nối tri thức hay khác:

• Giải SBT Toán 10 trang 32 Tập 2