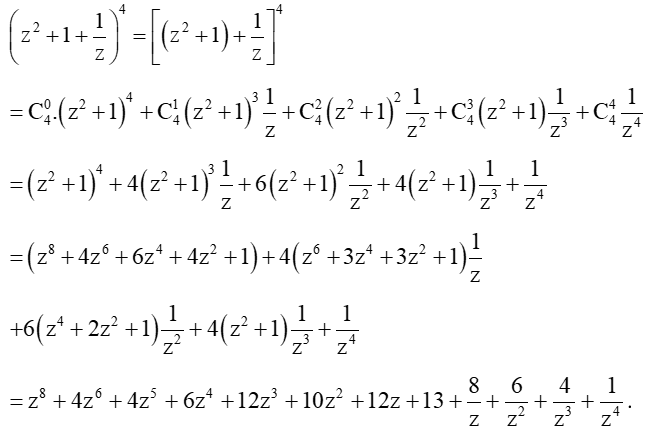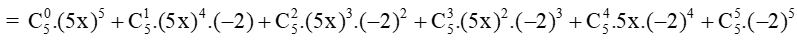Giải SBT Toán 10 trang 57 Tập 2 Kết nối tri thức

---

Với Giải SBT Toán 10 trang 57 Tập 2 trong Bài 25: Nhị thức Newton Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 57.

Giải SBT Toán 10 trang 57 Tập 2 Kết nối tri thức

Bài 8.13 trang 57 Sách bài tập Toán lớp 10 Tập 2: Khai triển các đa thức

a) (x – 2)⁴;

b) (x + 2)⁵;

c) (2x + 3y)⁴;

d) (2x – y)⁵.

Hướng dẫn giải:

a)

(x – 2)⁴ = [x + (– 2)⁴]

= $C_4^0.x^4+C_4^1.x^3.(-2)+C_4^2.x^2.{(-2)}^2+C_4^3.x.{(-2)}^3+C_4^4.{(-2)}^4$

= 1.x⁴ + 4.x³.(–2) + 6.x².4 + 4.x.(–8) + 1.16

= x⁴ – 8x³ + 24x² – 32x + 16.

b)

${\left(x+2\right)}^5$

$=C_5^0.x^5+C_5^1.x^4.2+C_5^2.x^3.2^2+C_5^3.x^2.2^3+C_5^4.x.2^4+C_5^5.2^5$

= 1.x⁵ + 5.x^4­.2 + 10.x³.4 + 10.x².8 + 5.x.16 + 1.32

= x⁵ + 10x⁴ + 40x³ + 80x² + 80x + 32.

c)

(2x + 3y)⁴

= $C_4^0.{\left(2x\right)}^4+C_4^1.{\left(2x\right)}^3.3y+C_4^2.{\left(2x\right)}^2.{\left(3y\right)}^2+C_4^3.2x.{\left(3y\right)}^3+C_4^4.{\left(3y\right)}^4$

= 1.16x⁴ + 4.8x³.3y + 6.4x².9y² + 4.2x.27y³ + 1.81y⁴

= 16x⁴ + 96x³y + 216x²y^2­ + 216xy³ + 81y⁴.

d)

(2x – y)⁵ = [2x + (– y)⁵]

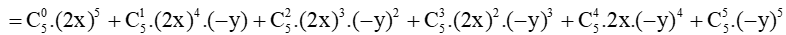
= 1.32x⁵ + 5.16x^4­.(–y) + 10.8x³.y² + 10.4x².(–y)³ + 5.2x.y⁴ + 1.(–y)⁵

= 32x⁵ – 80x⁴y + 80x³y² – 40x²y³ + 10xy⁴ – y⁵.

Bài 8.14 trang 57 Sách bài tập Toán lớp 10 Tập 2: Trong khai triển của (5x – 2)⁵, số mũ của x được sắp xếp theo luỹ thừa tăng dần, hãy tìm hạng tử thứ hai.

Hướng dẫn giải:

Áp dụng công thức khai triển của (a + b)⁵ với a = 5x, b = –2, ta có:

(5x – 2)⁵

= 1 . 3 125x⁵ + 5 . 625x^4­.(–2) + 10 . 125x³.4 + 10 . 25x².(–8) + 5 . 5x.16 + 1.(–32)

= 3 125x⁵ – 6 250x⁴ + 5 000x³ – 2 000x² + 400x – 32

= – 32 + 400x – 2 000x² + 5 000x³ – 6 250x⁴ + 3 125x⁵

Vậy, số hạng thứ hai trong khai triển theo số mũ tăng dần của x là 400x.

Bài 8.15 trang 57 Sách bài tập Toán lớp 10 Tập 2: Hãy sử dụng ba số hạng đầu tiên trong khai triển của (1 + 0,03)⁴ để tính giá trị gần đúng của 1,03⁴. Xác định sai số tuyệt đối.

Hướng dẫn giải:

Ta có:

1,03⁴ = (1 + 0,03)⁴ = 1⁴ + 4.1³.0,03 + 6.1^2­­.(0,03)² + …

= 1 + 0,12 + 0,0054 + … ≈ 1,1254

Mặt khác, ta tính được giá trị đúng, chẳng hạn bằng máy tính,

1,03⁴ = 1,12550881.

Như vậy, sai số tuyệt đối của của giá trị gần đúng nhận được so với giá trị đúng là:

|1,1254 – 1,12550881| = 0,00010881.

Bài 8.16 trang 57 Sách bài tập Toán lớp 10 Tập 2: Xác định hạng tử không chứa x trong khai triển của ${\left(x+\frac{2}{x}\right)}^4$.

Hướng dẫn giải:

Ta có:

${\left(x+\frac{2}{x}\right)}^4$

$=C_4^0.x^4+C_4^1.x^3.\frac{2}{x}+C_4^2.x^2{\left(\frac{2}{x}\right)}^2+C_4^3.x.{\left(\frac{2}{x}\right)}^3+C_4^4.{\left(\frac{2}{x}\right)}^4$

$=x^4+4x^3.\frac{2}{x}+6x^2.{\left(\frac{2}{x}\right)}^2+4x.{\left(\frac{2}{x}\right)}^3+{\left(\frac{2}{x}\right)}^4$

$=x^4+8x^2+24+\frac{32}{x^2}+\frac{16}{x^4}$

Vậy, hạng tử không chứa x là 24.

Bài 8.17 trang 57 Sách bài tập Toán lớp 10 Tập 2: Khai triển ${\left(z^2+1+\frac{1}{z}\right)}^4$.

Hướng dẫn giải:

Trước hết, ta sử dụng công thức khai triển của (a + b)⁴ với a = z² + 1 và $b=\frac{1}{z}$.

Sau đó, ta sử dụng các công thức khai triển của (a + b)⁴, (a + b)³, (a + b)² với a = z², b = 1 để có:

${\left(z^2+1\right)}^4$

$=C_4^0.{\left(z^2\right)}^4+C_4^1.{\left(z^2\right)}^3.1+C_4^2.{\left(z^2\right)}^2.1^2+C_4^3.z^2.1^3+C_4^4.1^4$

= z⁸ + 4z⁶ + 6z⁴ + 4$z^2$ + 1

${\left(z^2+1\right)}^3=C_3^0.{\left(z^2\right)}^3+C_3^1.{\left(z^2\right)}^2.1+C_3^2.z^2.1^2+C_3^3.1^3$

= z⁶ + 3z⁴ + 3z² + 1

(z² + 1)² = z⁴ + 2z² + 1

Vậy ta có: