Giải SBT Toán 10 trang 70 Tập 2 Kết nối tri thức

---

Với Giải SBT Toán 10 trang 70 Tập 2 trong Bài tập ôn tập cuối năm Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 70.

Giải SBT Toán 10 trang 70 Tập 2 Kết nối tri thức

Bài 1 trang 70 Sách bài tập Toán lớp 10 Tập 2: Cho các mệnh đề:

P: “Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt”;

Q: “Phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0”.

a) Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q, 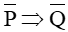. Xét tính đúng sai của các mệnh đề này.

b) Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.

c) Gọi X là tập hợp các phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt, Y là tập hợp các phương trình bậc hai ax² + bx + c = 0 có hệ số a và c trái dấu. Nêu mối quan hệ giữa hai tập hợp X và Y.

Hướng dẫn giải:

a)

+ Mệnh đề P ⇒ Q: “Nếu phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt thì phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0”. Đây là mệnh đề đúng.

+ Mệnh đề Q ⇒ P: “ Nếu phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0 thì phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt”. Đây là mệnh đề đúng.

+ Mệnh đề P ⇔ Q: “Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt khi và chỉ khi phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0”. Do P ⇒ Q, Q ⇒ P đều là các mệnh đề đúng nên mệnh đề P ⇔ Q là mệnh đề đúng.

+ Mệnh đề

Mệnh đề 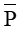là mệnh đề 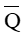phủ định của mệnh đề P và được phát biểu là: “Phương trình bậc hai ax² + bx + c = 0 không có hai nghiệm phân biệt”.

Mệnh đề là mệnh đề phủ định của mệnh đề Q và được phát biểu là: “Phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac ≤ 0”.

Khi đó, ta phát biểu mệnh đề 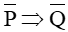: “Nếu phương trình bậc hai ax² + bx + c = 0 không có hai nghiệm phân biệt thì phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac ≤ 0”. Mệnh đề này là mệnh đề đúng.

b)

+ Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt là điều kiện đủ để phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0.

+ Phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0 là điều kiện cần để phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt.

c) Ta có các phương trình bậc hai ax² + bx + c = 0 có hệ số a và c trái dấu thì luôn có hai nghiệm trái dấu, hiển nhiên đây là hai nghiệm phân biệt. Nhưng các phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt thì hai nghiệm này chưa chắc đã trái dấu.

Do đó mọi phần tử của tập hợp Y thì đều là phần tử của tập hợp X.

Vậy Y là tập con của tập hợp X và ta viết Y ⊂ X.

Bài 2 trang 70 Sách bài tập Toán lớp 10 Tập 2:

a) Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:

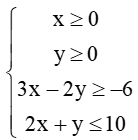
b) Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D.

Hướng dẫn giải:

a) Ta xác định miền nghiệm của từng bất phương trình trong hệ đã cho như sau:

Bước 1: Trục Oy có phương trình x = 0 và điểm (1; 0) thỏa mãn 1 > 0. Do đó miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (miền không bị gạch).

Bước 2: Trục Ox có phương trình y = 0 và điểm (0; 1) thỏa mãn 1 > 0. Do đó, miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1) (miền không bị gạch).

Bước 3: Vẽ đường thẳng d₁: 3x – 2y = – 6. Lấy điểm O(0; 0) không thuộc d₁ và thay x = 0, y = 0 vào biểu thức 3x – 2y ta được: 3 . 0 – 2 . 0 = 0 > – 6. Do đó, miền nghiệm của bất phương trình 3x – 2y ≥ – 6 là nửa mặt phẳng bờ d₁ chứa điểm O(0; 0) (miền không bị gạch).

Bước 4: Vẽ đường thẳng d₂: 2x + y = 10. Lấy điểm O(0; 0) không thuộc d₂ và thay x = 0, y = 0 vào biểu thức 2x + y ta được: 2 . 0 + 0 = 0 < 10. Do đó, miền nghiệm của bất phương trình 2x + y ≤ 10 là nửa mặt phẳng bờ d₂ chứa điểm O(0; 0) (miền không bị gạch).

Vậy miền nghiệm D của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch), trong đó A(0; 3), B(2; 6), C(5; 0), như hình vẽ sau:

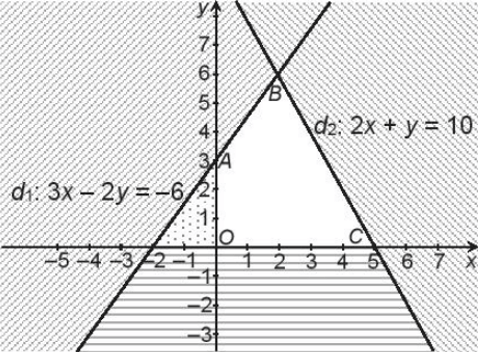
b) Vì giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D, do đó ta tính giá trị của F tại (x; y) là tọa độ các đỉnh O, A, B, C.

Ta có: F(0; 0) = 2 . 0 + 3 . 0 = 0;

F(0; 3) = 2 . 0 + 3 . 3 = 9;

F(2; 6) = 2 . 2 + 3 . 6 = 22;

F(5; 0) = 2 . 5 + 3 . 0 = 10.

Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D lần lượt là 22 và 0.

Bài 3 trang 70 Sách bài tập Toán lớp 10 Tập 2: Cho tam thức bậc hai f(x) = ax² + bx + c với đồ thị là parabol có đỉnh I(1; 4) và đi qua điểm A(2; 3).

a) Xác định các hệ số a, b, c của tam thức bậc hai f(x).

b) Vẽ parabol này.

c) Từ đồ thị đã vẽ ở câu b), hãy cho biết khoảng đồng biến, khoảng nghịch biến và tập giá trị của hàm số y = f(x).

d) Lập bảng xét dấu để giải bất phương trình $\frac{f\left(x\right)}{x-2}\ge 0$.

Hướng dẫn giải:

a) Parabol có đỉnh là I(1; 4) nên có phương trình dạng y = a(x – 1)² + 4.

Vì điểm A(2; 3) thuộc parabol nên ta có:

3 = a(2 – 1)² + 4 ⇔ a + 4 = 3 ⇔ a = – 1.

Vậy tam thức bậc hai cần tìm là f(x) = –(x – 1)² + 4 hay f(x) = – x² + 2x + 3.

Suy ra các hệ số là: a = – 1; b = 2; c = 3.

b) Ta có: a = – 1 < 0 nên parabol quay bề lõm xuống dưới.

Đỉnh parabol là I(1; 4).

Trục đối xứng x = 1.

Giao điểm của parabol với trục Oy là (0; 3). Điểm đối xứng với điểm (0; 3) qua trục đối xứng x = 1 là (2; 3).

Giao điểm của parabol với trục Ox là (– 1; 0) và (3; 0).

Vẽ đường cong đi qua các điểm trên ta được parabol cần vẽ.

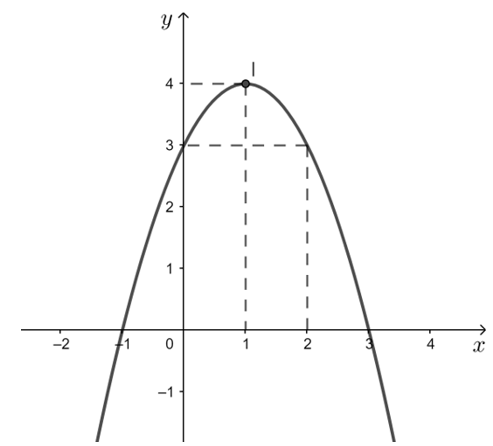
c) Từ đồ thị trên ta thấy:

- Hàm số đồng biến trên khoảng (– ∞; 1) và nghịch biến trên khoảng (1; + ∞).

- Tập giá trị của hàm số là (– ∞; 4].

d) Xét bất phương trình $\frac{f\left(x\right)}{x-2}\ge 0$, hay $\frac{-x^2+2x+3}{x-2}\ge 0$.

Tam thức f(x) = – x² + 2x + 3 có ∆' = 1² – (– 1) . 3 = 4 > 0 và a = – 1 < 0, f(x) có hai nghiệm phân biệt x₁ = – 1 và x₂ = 3. Do đó, f(x) > 0 với mọi x ∈ (– 1; 3) và f(x) < 0 với mọi x ∈ (– ∞; – 1) ∪ (3; + ∞).

Ta có bảng xét dấu sau:

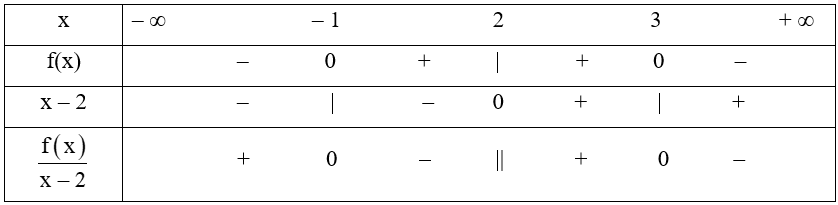
Vậy tập nghiệm của bất phương trình đã cho là S = (– ∞; – 1] ∪ (2; 3].

Lời giải sách bài tập Toán lớp 10 Bài tập ôn tập cuối năm Kết nối tri thức hay khác:

• Giải SBT Toán 10 trang 71 Tập 2

• Giải SBT Toán 10 trang 72 Tập 2

• Giải SBT Toán 10 trang 73 Tập 2