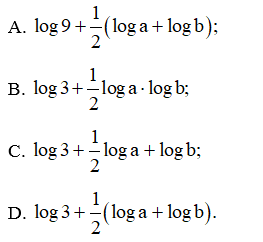Cho a > 0, b > 0 thỏa mãn a^2 + b^2 = 7ab

Cho a > 0, b > 0 thỏa mãn a + b = 7ab. Khi đó, log(a+b) bằng:

Giải sách bài tập Toán 11 Bài 2: Phép tính lôgarit

Bài 26 trang 38 SBT Toán 11 Tập 2: Cho a > 0, b > 0 thỏa mãn a² + b² = 7ab. Khi đó, log(a+b) bằng:

Lời giải:

Đáp án đúng là: D

Với a > 0, b > 0 ta có:

a² + b² = 7ab hay a² + 2ab + b² = 9ab ⇒ (a + b)² = 9ab.

$\Rightarrow a+b=\sqrt{9ab}\Rightarrow a+b=3{\left(ab\right)}^{\frac{1}{2}}$ (Vì a > 0, b > 0).

Xét: $\log \left(a+b\right)=\log \left[3{\left(ab\right)}^{\frac{1}{2}}\right]$

                         $=\log 3+\log {\left(ab\right)}^{\frac{1}{2}}$

                         $=\log 3+\frac{1}{2}\left(\log a+\log b\right).$

Lời giải SBT Toán 11 Bài 2: Phép tính lôgarit hay khác:

• Bài 17 trang 37 SBT Toán 11 Tập 2: Cho a > 0, a ≠ 2. Giá trị của ${\log }_{\frac{a}{2}}\left(\frac{a^2}{4}\right)$ bằng:....

• Bài 18 trang 37 SBT Toán 11 Tập 2: Cho a > 0, a ≠ 1. Giá trị của ${\log }_a\sqrt{a\sqrt{a}}$ bằng:...

• Bài 19 trang 37 SBT Toán 11 Tập 2: Cho a > 0. Giá trị của ${\log }_2\left(\frac{8}{a}\right)$ bằng:....

• Bài 20 trang 37 SBT Toán 11 Tập 2: Nếu log_ab = 2, log_ac = 3, thì log_a(b²c³) bằng:....

• Bài 21 trang 38 SBT Toán 11 Tập 2: Cho a > 0. Giá trị của ln(9a) – ln(3a) bằng:....

• Bài 22 trang 38 SBT Toán 11 Tập 2: Cho a > 0, b > 0. Mệnh đề đúng là:...

• Bài 23 trang 38 SBT Toán 11 Tập 2: Cho a > 0, a ≠ 1 và b > 0. Mệnh đề đúng là:....

• Bài 24 trang 38 SBT Toán 11 Tập 2: Nếu log₂3 = a thì log₆9 bằng:....

• Bài 25 trang 38 SBT Toán 11 Tập 2: Nếu log_ab = 5 thì ${\log }_{a^{2}b}\left(a{b}^2\right)$ bằng:....

• Bài 27 trang 38 SBT Toán 11 Tập 2: Không sử dụng máy tính cầm tay, hãy tính:a) ${\log }_{\sqrt{2}}8;$ ....

• Bài 28 trang 38 SBT Toán 11 Tập 2: Tính:a,$A=\frac{{25}^{{\log }_{5}6}+{49}^{{\log }_{7}8}-3}{3^{1+{\log }_{9}4}+4^{2-{\log }_{2}3}+5^{{\log }_{125}27}};$  ....

• Bài 29 trang 39 SBT Toán 11 Tập 2: Cho log_ab = 4. Tính:....

• Bài 30 trang 39 SBT Toán 11 Tập 2: a) Cho log₂3 = a. Tính log₁₈72 theo a.....

• Bài 31 trang 39 SBT Toán 11 Tập 2: Cho x > 0, y > 0 thoả mãn: x² + 4y² = 6xy. Chứng minh rằng:....

• Bài 32 trang 39 SBT Toán 11 Tập 2: Cho a, b, c, x, y, z là các số thực dương khác 1 và log_xa, log_yb, log_zc theo thứ tự lập thành một cấp số cộng....

• Bài 33 trang 39 SBT Toán 11 Tập 2: Để tính độ tuổi của mẫu vật bằng gỗ, người ta đo độ phóng xạ....