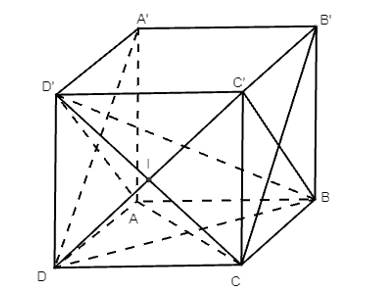
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính:
Giải sách bài tập Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
Bài 55 trang 117 SBT Toán 11 Tập 2: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính:
a) Khoảng cách giữa hai mặt phẳng (ABCD) và (A’B’C’D’);
b) Số đo của góc nhị diện [A, CD, B’];
c) Tang của góc giữa đường thẳng BD’ và mặt phẳng (ABCD);
d) Khoảng cách giữa hai đường thẳng C’D và BC;
e*) Góc giữa hai đường thẳng BC’ và CD’.
Lời giải:
Ta có: ABCD.A’B’C’D’ là hình lập phương cạnh a nên tất cả các mặt bên và hai mặt đáy của hình lập phương ABCD. A’B’C’D’ đều là hình vuông cạnh a.
a) Do ABCD.A’B’C’D’ là hình lập phương nên ta có (ABCD) // (A’B’C’D’) và AA’ ⊥ (ABCD).
Như vậy: d((ABCD), (A’B’C’D’)) = d(A’, (ABCD)) = AA’ = a.
b) Do ABCD.A’B’C’D’ là hình lập phương nên ta có A’B’ // DC.
Suy ra bốn điểm A’, B’, C, D đồng phẳng.
Khi đó, góc nhị diện [A, CD, B’] bằng góc nhị diện [A, CD, A’].
Ta có: CD ⊥ AD, CD ⊥ DD’ (do ABCD, D’C’CD là hai hình vuông), AD ∩ DD’ = D trong (A’D’DA).
Suy ra CD ⊥ (A’D’DA).
Hơn nữa A’D ⊂ (A’D’DA).
Nên ta có CD ⊥ A’D.
Ta thấy: A’D ⊥ CD, AD ⊥ CD (do ABCD là hình vuông), AD ∩ A’D = D ∈ CD.
Suy ra là góc phẳng nhị diện của góc nhị diện [A, CD, A’] hay góc nhị diện [A, CD, B’].
Vì ADD’A là hình vuông nên
Vậy số đo của góc nhị diện [A, CD, B’] bằng 45°
c) Vì DD’ ⊥ (ABCD) nên góc giữa đường thẳng BD’ và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng BD’ và BD và bằng
Do ABCD là hình vuông cạnh a, nên ta có
Ta có: DD’ ⊥ (ABCD), BD ⊂ (ABCD) nên DD’ ⊥ BD.
Xét tam giác D’DB vuông tại D có:
Vậy tang của góc giữa đường thẳng BD’ và mặt phẳng (ABCD) bằng
d) Gọi I là giao điểm của CD’ và C’D.
Do D’C’CD là hình vuông nên I là trung điểm của CD’ và CD’ ⊥ C’D hay IC ⊥ C’D.
Ta có: BC ⊥ (D’C’CD) (do ABCD.A’B’C’D’ là hình lập phương)
Mà IC ⊂ (D’C’CD) nên BC ⊥ IC.
Ta thấy: IC ⊥ C’D, IC ⊥ BC nên IC là đoạn vuông góc chung của hai đường thẳng C’D và BC.
Như vậy:
Do ABCD, D’C’CD, A’D’DA là các hình vuông cạnh a nên có các đường chéo
Suy ra
Vậy khoảng cách giữa hai đường thẳng C’D và BC bằng
e*) Ta có: D’C’ song song và bằng DC, DC song song và bằng AB (do DC’CD, ABCD là hai hình vuông cạnh a), nên D’C’ song song và bằng AB.
Suy ra ABC’D’ là hình bình hành nên ta có BC’ // AD’.
Khi đó góc giữa hai đường thẳng BC’ và CD’ bằng góc giữa hai đường thẳng AD’ và CD’ và bằng
Vì nên tam giác ACD’ là tam giác đều.
Suy ra
Vậy góc giữa hai đường thẳng BC’ và CD’ bằng 60°.
Lời giải SBT Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối hay khác: