Cho hình chóp S ABC có SA ⊥ (ABC) Tam giác ABC vuông tại A góc ABC = 30° AC = a

Cho hình chóp S.ABC có SA ⊥ (ABC). Tam giác ABC vuông tại A, , AC = a, . Tính số đo góc phẳng nhị diện [S, BC, A].

Giải sách bài tập Toán 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện - Chân trời sáng tạo

Bài 4 trang 73 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Tam giác ABC vuông tại A, $\widehat{AB\text{}C}=30°$, AC = a, $SA=\frac{a\sqrt{3}}{2}$. Tính số đo góc phẳng nhị diện [S, BC, A].

Lời giải:

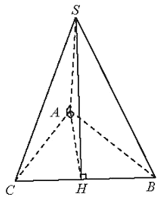
Vẽ AH ⊥ BC (H ϵ BC), ta có SH ⊥ BC.

Suy ra $\widehat{SHA}$ là góc phẳng nhị diện [S, BC, A].

Ta có AH = AC.sin60° = $\frac{a\sqrt{3}}{2}$= SA

Do đó $\widehat{SHA}$ = 45°.

Lời giải SBT Toán 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện hay khác:

• Bài 1 trang 73 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là hình vuông tâm O cạnh a, SA = $a\sqrt{3}$  và vuông góc với đáy. Xác định và tính góc giữa: ....

• Bài 2 trang 73 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 3. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm I của cạnh AB ....

• Bài 3 trang 73 SBT Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng $\frac{a\sqrt{15}}{6}$ . Tính số đo góc phẳng nhị diện [S, BC, A]. ....