Cho góc xOy bằng 45 độ và điểm M nằm trong góc xOy

Giải sách bài tập Toán lớp 7 Bài 5: Đường trung trực của một đoạn thẳng

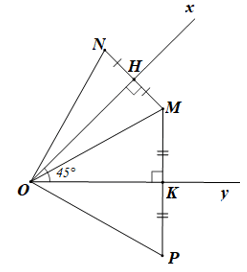
Bài 2 trang 55 sách bài tập Toán lớp 7 Tập 2: Cho góc xOy bằng 45° và điểm M nằm trong góc xOy. Vẽ điểm N sao cho Ox là trung trực của MN, vẽ điểm P sao cho Oy là trung trực của MP.

a) Chứng minh ON = OP.

b) Tính số đo góc NOP.

Lời giải:

a) Ta có Ox là trung trực của MN (giả thiết).

Suy ra OM = ON (tính chất đường trung trực của một đoạn thẳng).

Vì Oy là trung trực của MP (giả thiết).

Nên OM = OP (tính chất đường trung trực của một đoạn thẳng).

Suy ra ON = OP (= OM).

Vậy ON = OP.

b) Gọi H và K lần lượt là trung điểm của MN và MP.

Xét tam giác ONH và tam giác OMH có:

ON = OM (chứng minh câu a),

NH = MH (do H là trung điểm của MN),

OH là cạnh chung.

Do đó ∆ONH = ∆OMH (c.c.c).

Suy ra $\widehat{NOH}=\widehat{MOH}$ (hai góc tương ứng).

Tương tự ta có: ∆OKM = ∆OKP (c.c.c).

Suy ra $\widehat{KOM}=\widehat{K\text{O}P}$ (hai góc tương ứng).

Ta có $\widehat{NOP}=\widehat{NOH}+\widehat{MOH}+\widehat{K\text{O}M}+\widehat{K\text{O}P}$

Mà $\widehat{NOH}=\widehat{MOH}$, $\widehat{KOM}=\widehat{K\text{O}P}$ (chứng minh trên).

Nên $\widehat{NOP}=2\widehat{MOH}+2\widehat{K\text{O}M}=2(\widehat{MOH}+\widehat{K\text{O}M})$

Hay $\widehat{NOP}=2\widehat{K\text{OH}}=2.45°=90°$.

Vậy $\widehat{NOP}=90°.$