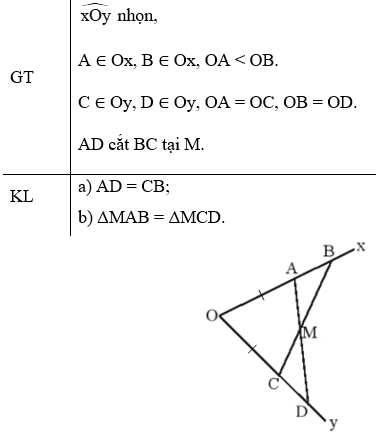
Cho góc xOy Lấy hai điểm A, B thuộc tia Ox sao cho OA nhỏ hơn OB

Giải sách bài tập Toán lớp 7 Bài 2: Tam giác bằng nhau

Bài 9 trang 46 sách bài tập Toán lớp 7 Tập 2: Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OA = OC, OB = OD. Gọi M là giao điểm của AD và CB. Chứng minh rằng:

a) AD = CB;

b) ΔMAB = ΔMCD.

Lời giải:

a) Xét ∆AOD và ∆COB có:

OA = OC (giả thiết),

$\hat{O}$ là góc chung,

OD = OB (giả thiết).

Do đó ΔAOD = ΔCOB (c.g.c).

Suy ra AD = CB (hai cạnh tương ứng).

Vậy AD = CB.

b) Ta có OB = OA + AB (do OA < OB) nên AB = OB – OA.

Tương tự OD = OC + CD nên CD = OD – OC.

Mà OA = OC, OB = OD (giả thiết).

Suy ra AB = CD.

Vì ΔAOD = ΔCOB (chứng minh câu a).

Nên $\widehat{A\text{D}O}=\widehat{CBO},\widehat{\text{DA}O}=\widehat{BCO}$ (các cặp góc tương ứng) (1)

Ta có $\widehat{DAO}+\widehat{DAB}=180°$ (hai góc kề bù)

Suy ra $\widehat{DAB}=180°-\widehat{DAO}$ (2)

Ta có $\widehat{BCO}+\widehat{BC\text{D}}=180°$ (hai góc kề bù)

Hay $\widehat{BC\text{D}}=180°-\widehat{BCO}$ (3)

Từ (1),(2),(3) suy ra $\widehat{\text{DAB}}=\widehat{BCD}$.

Xét ΔMAB và ΔMCD có

$\widehat{\text{MAB}}=\widehat{MCD}$ (do $\widehat{\text{DAB}}=\widehat{BCD}$),

AB = CD (chứng minh trên),

$\widehat{MBA}=\widehat{M\text{D}C}$ (do $\widehat{CBO}=\widehat{A\text{D}O}$).

Do đó ΔMAB = ΔMCD (g.c.g).

Vậy ΔMAB = ΔMCD.