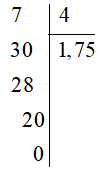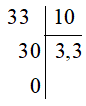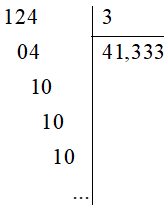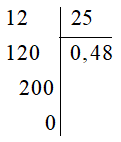Giải SBT Toán 7 trang 35 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 7 trang 35 Tập 1 trong Bài 1: Số vô tỉ. Căn bậc hai số học Sách bài tập Toán lớp 7 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 35.

Giải SBT Toán 7 trang 35 Tập 1 Chân trời sáng tạo

Bài 1 trang 35 sách bài tập Toán lớp 7 Tập 1:

a) Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân.

$-\frac{7}{4};$ $\frac{33}{10};$ $-\frac{124}{3};$ $\frac{12}{25}.$

b) Trong các số thập phân trên hãy chỉ ra các số thập phân vô hạn tuần hoàn.

Lời giải:

a) +) Đặt tính, ta được:

Vậy $-\frac{7}{4}=-1,75.$

+) Đặt tính, ta được:

Vậy $\frac{33}{10}=3,3.$

+) Đặt tính, ta được:

Vậy $-\frac{124}{3}=$ 9 – 41,333... = – 41,(3).

Đặt tính, ta được:

Vậy $\frac{12}{25}=0,48.$

b) Trong các số thập phân trên, số thập phân vô hạn tuần hoàn là – 41, 333... .

Bài 2 trang 35 sách bài tập Toán lớp 7 Tập 1: Hãy biểu diễn các số thập phân sau dưới dạng số hữu tỉ: 7,2; 0,25; 7,(2).

Lời giải:

Ta có:

7,2 = $\frac{72}{10};$

0,25 = $\frac{25}{100};$

7,(2) = 7 + 0,(2) = 7 + 2.0,(1) = 7 + $2.\frac{1}{9}$ = $\frac{63}{9}+\frac{2}{9}=\frac{65}{9}$.

Vậy biểu diễn các số thập phân 7,2; 0,25; 7,(2) dưới dạng số hữu tỉ lần lượt là $\frac{72}{10};\frac{25}{100};\frac{65}{9}.$

Bài 3 trang 35 sách bài tập Toán lớp 7 Tập : Chọn phát biểu đúng trong các phát biểu sau:

a) $\sqrt{3}\in$𝕀;

b) $\sqrt{25}\in$𝕀;

c) – 𝛑∈𝕀;

d) $\sqrt{\frac{100}{47}}\in \mathbb{Q}.$

Lời giải:

a) Ta có: $\sqrt{3}\approx 1,\mathrm{732050808...}$ nên $\sqrt{3}$ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn. Suy ra $\sqrt{3}$ là số vô tỉ hay $\sqrt{3}\in$ 𝕀. Do đó a) đúng.

b) Ta có 5² = 25 (5 > 0) nên $\sqrt{25}=5$. Suy ra $\sqrt{5}$ là số hữu tỉ, mà số hữu tỉ không phải số cô tỉ nên $\sqrt{25}\notin$ 𝕀. Do đó b) sai.

c) Ta có: – π ≈ -3,141592654... nên – π được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn. Suy ra – π là số vô tỉ hay – π ∈𝕀. Do đó c) đúng.

d) Ta có: $\sqrt{\frac{100}{47}}\approx 1,\mathrm{458649915...}$ nên $\sqrt{\frac{100}{47}}$ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn. Suy ra $\sqrt{\frac{100}{47}}$ là số vô tỉ, mà số vô tỉ không là số hữu tỉ. Do đó d) sai.

Vậy phát biểu đúng là a và c.

Bài 4 trang 35 sách bài tập Toán lớp 7 Tập 1: Tính:

a) $-\sqrt{81};$

b) $\sqrt{225};$

c) $\sqrt{\frac{64}{25}};$

d) $\sqrt{{\left(-11\right)}^2};$

e) $\sqrt{{\left(13\right)}^2}.$

Lời giải:

a) Ta có 9² = 81 (9 > 0) nên $-\sqrt{81}=-9.$

b) Ta có: 15² = 225 (15 > 0) nên $\sqrt{225}=15.$

c) Ta có: ${\left(\frac{8}{5}\right)}^2=\frac{8}{5}.\frac{8}{5}=\frac{64}{25}$ nên $\sqrt{\frac{64}{25}}=\frac{8}{5}.$

d) Ta có 11² = (-11)² (11 > 0) nên $\sqrt{{\left(-11\right)}^2}=11$

e) Ta có 13 > 0 nên $\sqrt{{\left(13\right)}^2}=13.$

Bài 5 trang 35 sách bài tập Toán lớp 7 Tập 1: Hãy thay dấu ? bằng các số thích hợp:

a	256	?	36	?
$\sqrt{a}$	?	7	?	20

Lời giải:

Ta có:

16² = 256 (16 > 0) nên $\sqrt{256}=16$ . Do đó $\sqrt{a}$ = 16.

7² = 49 nên a = 49.

6² = 36 (6 > 0) nên $\sqrt{36}=6$ . Do đó a = 6.

20² = 400 nên a = 400.

Khi đó ta điền vào bảng, ta được:

a	256	49	36	400
$\sqrt{a}$	16	7	6	20

Lời giải sách bài tập Toán lớp 7 Bài 1: Số vô tỉ. Căn bậc hai số học Chân trời sáng tạo hay khác:

• Giải SBT Toán 7 trang 36 Tập 1