Giải SBT Toán 7 trang 63 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 7 trang 63 Tập 1 trong Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác Sách bài tập Toán lớp 7 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 63.

Giải SBT Toán 7 trang 63 Tập 1 Chân trời sáng tạo

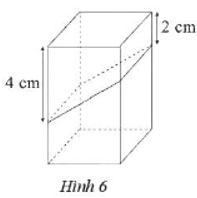
Bài 1 trang 63 sách bài tập Toán lớp 7 Tập 1: Một chiếc hộp hình hộp chữ nhật có đáy là hình vuông cạnh 3 cm, chiều cao 7 cm. Nam cắt chiếc hộp thành hai hình lăng trụ đứng tứ giác với kích thước các đoạn cắt trên như Hình 6.

Tính thể tích của hai hình lăng trụ đứng tứ giác sau khi cắt.

Lời giải:

Quan sát Hình 6 ta thấy hai hình lăng trụ vừa cắt là hai hình lăng trụ đứng tứ giác có đáy là hình thang.

Hình lăng trụ đứng phía trên có chiều cao h₁ = 3 cm và đáy là hình thang có các kích thước là 4 cm (đáy lớn), 2 cm (đáy bé), 3 cm (chiều cao hình thang).

Diện tích đáy của hình lăng trụ đứng ở phía trên là: S₁ = (4 + 2) . 3 : 2 = 9 (cm²).

Thể tích của hình lăng trụ đứng ở phía trên là: V₁ = S₁ . h₁ = 9 . 3 = 27 (cm³).

Thể tích của hình hộp chữ nhật là: V = 3 . 3 . 7 = 63 (cm³).

Thể tích của hình lăng trụ đứng ở phía dưới là: V₂ = V – V₁ = 63 – 27 = 36 (cm³).

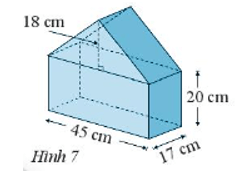
Bài 2 trang 63 sách bài tập Toán lớp 7 Tập 1: Mô hình một ngôi nhà có kích thước như Hình 7. Tính thể tích của mô hình ngôi nhà.

Lời giải:

Cách 1:

Quan sát Hình 7 ta thấy mô hình ngôi nhà gồm hai hình lăng trụ đứng (lăng trụ đứng tam giác và lăng trụ đứng tứ giác) ghép với nhau cùng có chiều cao là h = 17 cm.

+ Hình lăng trụ đứng tứ giác có đáy là hình chữ nhật với các kích thước là 45 cm và 20 cm nên diện tích đáy này là: S₁ = 45 . 20 = 900 (cm²).

Thể tích hình lăng trụ đứng tứ giác là: V₁ = S₁ . h = 900 . 17 = 15 300 (cm³).

+ Hình lăng trụ đứng tam giác có đáy là tam giác có chiều cao là 18 cm và cạnh đáy ứng với chiều cao đó có độ dài là 45 cm nên diện tích đáy này là: S₂ = $\frac{1}{2}$ . 18 . 45 = 405 (cm²).

Thể tích hình lăng trụ đứng tam giác là: V₂ = S₂ . h = 405 . 17 = 6 885 (cm³).

Vậy thể tích của mô hình ngôi nhà là: V = V₁ + V₂ = 15 300 + 6 885 = 22 185 (cm³).

Cách 2:

Có thể xem mô hình ngôi nhà là hình lăng trụ có đáy là hình gồm một tứ giác và tam giác ghép lại và chiều cao h = 17 cm.

Diện tích mặt đáy là: S = 45 . 20 + $\frac{1}{2}$ . 18 . 45 = 1 305 (cm²).

Thể tích của mô hình ngôi nhà là: V = S . h = 1 305 . 17 = 22 185 (cm³).

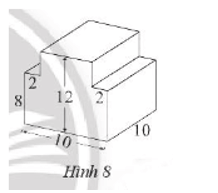
Bài 3 trang 63 sách bài tập Toán lớp 7 Tập 1: Một khối gỗ có kích thước như Hình 8 (đơn vị dm).

a) Tính thể tích của khối gỗ.

b) Tính diện tích toàn phần của khối gỗ.

Lời giải:

a) Quan sát Hình 8 ta thấy khối gỗ được ghép bởi hai khối hộp chữ nhật.

+ Khối hộp chữ nhật ở phía dưới có kích thước là 10 dm, 8 dm và 10 dm, do đó thể tích của khối hộp chữ nhật phía dưới là: V₁ = 10 . 8 . 10 = 800 (dm³).

+ Khối hộp chữ nhật ở phía trên có:

- Chiều dài là 10 dm;

- Chiều rộng là: 10 – 2 – 2 = 6 (dm);

- Chiều cao là: 12 – 8 = 4 (dm).

Thể tích của khối hộp chữ nhật ở phía trên là: V₂ = 10 . 6 . 4 = 240 (dm³).

Vậy thể tích của khối gỗ là V = V₁ + V₂ = 800 + 240 = 1 040 (dm³).

b) Có thể xem khối gỗ là hình lăng trụ có đáy hình gồm 2 hình chữ nhật ghép lại với nhau và chiều cao là h = 10 dm.

Chu vi đáy là: CV_đáy = 10 + 8 + 2 + 4 + 6 + 4 + 2 + 8 = 44 (dm).

Diện tích xung quanh của khối gỗ là: S_xq = CV_đáy . h = 44 . 10 = 440 (dm²).

Diện tích hai mặt đáy là: S_2đáy = 2 . (10 . 8 + 6 . 4) = 208 (dm²).

Diện tích toàn phần của khối gỗ là: S_tp = S_xq + S_2đáy = 440 + 208 = 648 (dm²).

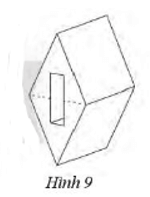
Bài 4 trang 63 sách bài tập Toán lớp 7 Tập 1: Một chi tiết máy bằng thép hình lăng trụ đứng tứ giác có đáy là một hình thoi có độ dài hai đường chéo là 16 cm và 18 cm, chiều cao 10 cm. Người ta khoét một lỗ hình hộp chữ nhật (Hình 9) có kích thước hai cạnh đáy là 2 cm và 6 cm. Tính thể tích còn lại của khối thép.

Lời giải:

Diện tích đáy hình thoi của khối lăng trụ là: S_đ = $\frac{1}{2}$ . 16 . 18 = 144 (cm²).

Thể tích của hình lăng trụ có đáy là hình thoi là: V = 144 . 10 = 1 440 (cm³).

Lỗ hình hộp chữ nhật có kích thước hai cạnh đáy là 2 cm và 6 cm và chiều cao chính bằng chiều cao của hình lăng trụ có đáy là hình thoi và là 10 cm. Do đó, thể tích cái lỗ hình hộp chữ nhật là: V_l = 2 . 6 . 10 = 120 (cm³).

Thể tích còn lại của khối thép là: V_cl = V – V_l = 1 440 – 120 = 1 320 (cm³).

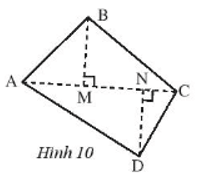
Bài 5 trang 63 sách bài tập Toán lớp 7 Tập 1: Tính thể tích của một hình lăng trụ đứng đáy là một tứ giác như Hình 10, có độ dài AC = 5 m, BM = DN = 3 m, chiều cao của lăng trụ 7 m.

Lời giải:

Từ Hình 10, ta thấy đáy của hình lăng trụ là một tứ giác, ta chia tứ giác đó thành 2 tam giác.

Tam giác ABC có chiều cao BM = 3 m và cạnh đáy AC = 5 m, diện tích tam giác ABC là:

S_ABC = $\frac{1}{2}$. BM . AC = $\frac{1}{2}$ . 3 . 5 = $\frac{15}{2}$ (m²).

Tam giác ADC có chiều cao DN = 3 m và cạnh đáy AC = 5 m, diện tích tam giác ADC là:

S_ADC = $\frac{1}{2}$ . DN . AC = $\frac{1}{2}$ . 3 . 5 = $\frac{15}{2}$ (m²).

Diện tích đáy của hình lăng trụ đã cho là: S_đ = S_ABC + S_ADC = $\frac{15}{2}$ + $\frac{15}{2}$ = 15 (m²).

Thể tích của hình lăng trụ là: V = S_đ . h = 15 . 7 = 105 (m³).

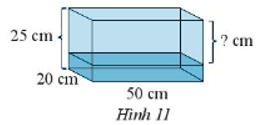
Bài 6 trang 63 sách bài tập Toán lớp 7 Tập 1: Một bể cá có kích thước như Hình 11, người ta đổ vào đó 6,25 lít nước. Khoảng cách từ mực nước đến miệng bể là bao nhiêu?

Lời giải:

Bể cá có dạng hình hộp chữ nhật có các kích thước là 20 cm, 50 cm, 25 cm.

Thể tích của bể cá là: 20 . 50 . 25 = 25 000 (cm³).

Đổi: 6,25 lít = 6,25 dm³ = 6 250 cm³.

Thể tích phần bể không chứa nước là: 25 000 – 6 250 = 18 750 (cm³).

Phần bể không chứa nước có dạng hình hộp chữ nhật có kích thước đáy giống bể cá và chiều cao chính là khoảng cách từ mực nước đến miệng bể.

Vậy khoảng cách từ mực nước đến miệng bể là: $\frac{18750}{20.50}=18,75$ (cm).

Lời giải sách bài tập Toán lớp 7 Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác Chân trời sáng tạo hay khác:

• Giải SBT Toán 7 trang 64 Tập 1