Giải SBT Toán 7 trang 45 Tập 2 Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm lời giải SBT Toán 7 trang 45 Tập 2 trong Bài 2: Tam giác bằng nhau Sách bài tập Toán lớp 7 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 45.
Giải SBT Toán 7 trang 45 Tập 2 Chân trời sáng tạo
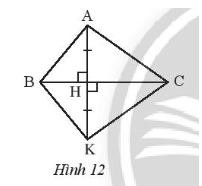
Bài 1 trang 45 sách bài tập Toán lớp 7 Tập 2: Trong Hình 12, tìm tam giác bằng tam giác ABH.
Lời giải:
Xét DABH và DKBH có:
(cùng bằng 90°),
BH là cạnh chung,
AH = HK (giả thiết).
Do đó ΔABH = ΔKBH (hai cạnh góc vuông).
Vậy ΔABH = ΔKBH.
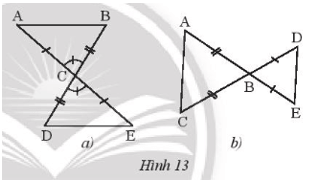
Bài 2 trang 45 sách bài tập Toán lớp 7 Tập 2: Hai tam giác trong Hình 13a, 13b có bằng nhau không? Vì sao?
Lời giải:
•Hình 13a)
Xét ∆ABC và ∆EDC có:
AC = EC (giả thiết),
(hai góc đối đỉnh),
BC = DC (giả thiết)
Do đó ΔABC = ΔEDC (c.g.c)
Vậy ΔABC = ΔEDC.
•Hình 13b)
Xét DABC và DEDB có:
AB = BC ≠ BE = BD.
Do đó hai tam giác ABC và EBD không bằng nhau
Vậy hai tam giác ABC và EBD không bằng nhau.
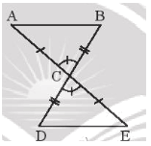
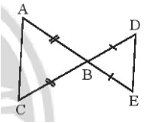
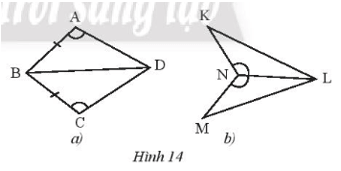
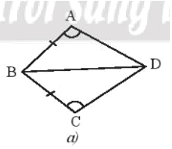
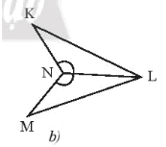
Bài 3 trang 45 sách bài tập Toán lớp 7 Tập 2: Nêu thêm điều kiện để hai tam giác trong Hình 14a, 14b bằng nhau theo trường hợp cạnh – góc – cạnh.
Lời giải:
•Hình a)
Để ∆ABD = ∆CBD theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.
Mà là góc xen kẽ giữa hai cạnh AB và AD, là góc xen kẽ giữa hai cạnh CB và CD.
Lại có AB = CB (giả thiết).
Do đó điều kiện còn lại là điều kiện về cạnh, đó là AD = CD.
Vậy cần thêm điều kiện AD = CD.
•Hình b)
Để ∆KNL = ∆MNL theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.
Mà là góc xen kẽ giữa hai cạnh NK và NL, là góc xen kẽ giữa hai cạnh NM và NL.
Lại có cạnh NL là cạnh chung của hai tam giác.
Do đó điều kiện còn lại là điều kiện về cạnh, đó là NK = NM.
Vậy cần thêm điều kiện NK = NM.
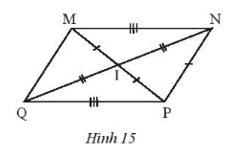
Bài 4 trang 45 sách bài tập Toán lớp 7 Tập 2: Quan sát Hình 15 rồi thay dấu ? bằng tên tam giác thích hợp.
a) ∆MNI = ∆?;
b) ∆INM = ∆?;
c) ∆? = ∆QIP.
Lời giải:
a) Xét ∆MNI và ∆PQI có:
MN = PQ (giả thiết),
MI = PI (giả thiết),
NI = QI (giả thiết).
Do đó ΔMNI = ΔPQI (c.c.c).
Vậy ΔMNI = ΔPQI.
b) Vì ΔMNI = ΔPQI (theo câu a) nên ΔINM =ΔIQP.
Vậy ΔINM =ΔIQP.
c) Vì ΔMNI = ΔPQI (theo câu a) nên ΔNIM = ΔQIP.
Vậy ΔNIM = ΔQIP.
Lời giải Sách bài tập Toán 7 Chân trời sáng tạo Bài 2: Tam giác bằng nhau Chân trời sáng tạo hay khác: