Giải SBT Toán 7 trang 63 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 7 trang 63 Tập 2 trong Bài 8: Tính chất ba đường cao của tam giác Sách bài tập Toán lớp 7 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 63.

Giải SBT Toán 7 trang 63 Tập 2 Chân trời sáng tạo

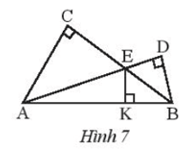
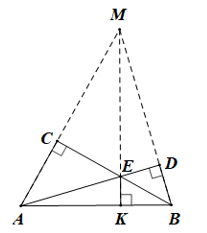
Bài 1 trang 63 sách bài tập Toán lớp 7 Tập 2: Trong Hình 7. Hãy chứng minh AC, EK và BD cùng đi qua một điểm.

Lời giải:

Gọi M là giao điểm của AC và BD.

Xét tam giác MAB có E là giao điểm của hai đường cao AD và BC nên E là trực tâm của tam giác MAB.

Khi đó ME là đường cao kẻ từ đỉnh M của tam giác AMB, tức là ME ⊥ AB.

Mà EK ⊥ AB.

Do đó EK đi qua điểm M.

Vậy AC, EK và BD cùng đi qua điểm M.

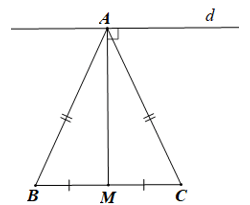
Bài 2 trang 63 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A, vẽ đường trung tuyến AM. Qua A vẽ đường thẳng d vuông góc với AM. Chứng minh d // BC.

Lời giải:

Vì tam giác ABC cân tại A (giả thiết) nên AB = AC.

Vì AM là trung tuyến của tam giác ABC nên BM = CM.

Xét ΔAMB và ΔAMC có:

Cạnh AM là cạnh chung,

AB = AC (chứng minh trên),

BM = CM (chứng minh trên).

Do đó ΔAMB = ΔAMC (c.c.c).

Suy ra $\widehat{AMB}=\widehat{AMC}$ (hai góc tương ứng).

Lại có $\widehat{AMB}+\widehat{AMC}=180°$ (hai góc kề bù).

Nên $\widehat{AMB}=\widehat{AMC}=\frac{180°}{2}=90°$.

Hay AM ⊥BC.

Mà d ⊥ AM (giả thiết).

Suy ra d // BC (dấu hiệu nhận biết hai đường thẳng song song).

Vậy d // BC.

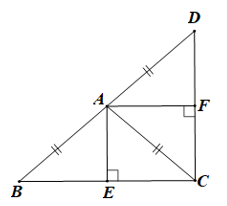
Bài 3 trang 63 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Vẽ hai đường cao AE và AF của hai tam giác ABC và ACD. Chứng minh góc EAF vuông.

Lời giải:

Vì tam giác ABC cân tại A nên AB = AC.

Mà AB = AD (vì A là trung điểm của BD).

Suy ra AC = AD = AB.

Xét ΔAEB và ΔAEC có:

$\widehat{AEB}=\widehat{AEC}\left(=90°\right)$,

Cạnh AE là cạnh chung,

AB = AC (chứng minh trên).

Do đó ΔAEB = ΔAEC (cạnh huyền – cạnh góc vuông).

Suy ra $\widehat{BA\text{E}}=\widehat{CA\text{E}}$ (hai góc tương ứng).

Xét ΔACF và ΔADF có:

$\widehat{AFC}=\widehat{AFD}\left(=90°\right)$,

Cạnh AF là cạnh chung,

AC = AD (chứng minh trên).

Do đó ΔAFC = ΔAFD (cạnh huyền – cạnh góc vuông).

Suy ra $\widehat{FAC}=\widehat{FAD}$ (hai góc tương ứng).

Ta có $\widehat{BA\text{E}}+\widehat{CA\text{E}}+\widehat{FAC}+\widehat{FAD}=180°$

Mà $\widehat{BA\text{E}}=\widehat{CA\text{E}}$, $\widehat{FAC}=\widehat{FAD}$(chứng minh trên).

Suy ra $2\widehat{EAC}+2\widehat{FAC}=180°$

Hay $2\left(\widehat{EAC}+\widehat{FAC}\right)=180°:2=90°$

Do đó $\widehat{EAF}=90°$.

Vậy góc EAF vuông.

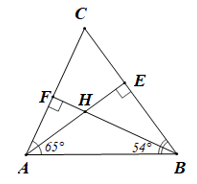
Bài 4 trang 63 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có $\hat{A}=65°,\hat{B}=54°$. Vẽ trực tâm H của tam giác ABC. Tính góc AHB.

Lời giải:

Trong tam giác vuông ABE ta có: $\widehat{E\text{A}B}+\widehat{EBA}=90°$ (trong một tam giác vuông, tổng hai góc nhọn bằng 90°).

Mà $\widehat{EBA}=54°$ nên $\widehat{EAB}=90°-\widehat{EBA}=90°-54°=36°$.

Trong tam giác vuông BAF ta có: $\widehat{\text{FA}B}+\widehat{FBA}=90°$ (trong một tam giác vuông, tổng hai góc nhọn bằng 90°).

Mà $\widehat{FAB}=65°$ nên $\widehat{FBA}=90°-\widehat{FAB}=90°-65°=25°$.

Trong ∆AHB ta có: $\widehat{HAB}+\widehat{HBA}+\widehat{AHB}=180°$ (tổng ba góc trong một tam giác).

Suy ra

$\widehat{AHB}=180°-\widehat{HAB}-\widehat{HBA}=180°-36°-25°=119°$.

Vậy $\widehat{AHB}=119°.$

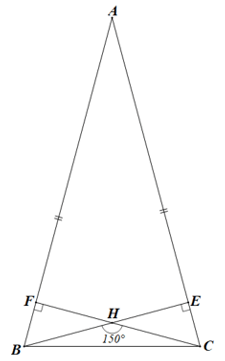
Bài 5 trang 63 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A có góc A nhọn và H là trực tâm. Cho biết $\widehat{BHC}=150°$. Tìm các góc của tam giác ABC.

Lời giải:

Vẽ hai đường cao BE và CF của tam giác ABC.

Trong ∆BHC có: $\widehat{HCB}+\widehat{HBC}+\widehat{CHB}=180°$ (tổng ba góc trong một tam giác).

Suy ra

$\widehat{HBC}+\widehat{HCB}=180-\widehat{BHC}=180°-150°=30°$

Trong ∆CBE vuông tại E có: $\widehat{ECB}+\widehat{EBC}=90°$ (trong một tam giác vuông, tổng hai góc nhọn bằng 90°).

Nên $\widehat{ECB}=90°-\widehat{EBC}$ (1)

Trong ∆CBF vuông tại F có: $\widehat{FCB}+\widehat{FBC}=90°$ (trong một tam giác vuông, tổng hai góc nhọn bằng 90°).

Nên $\widehat{FBC}=90°-\widehat{FCB}$ (2)

Từ (1) và (2) ta có:

$\widehat{FBC}+\widehat{ECB}=180°-\left(\widehat{EBC}+\widehat{FCB}\right)$

$=180°-\left(\widehat{HBC}+\widehat{HCB}\right)=180°-30°=150°.$

Hay $\widehat{ABC}+\widehat{ACB}=150°$

Do tam giác ABC cân tại A nên ta có:

$\widehat{ABC}=\widehat{ACB}=\frac{150°}{2}=75°$.

Trong ∆ABC có: $\widehat{ACB}+\widehat{ABC}+\widehat{CAB}=180°$ (tổng ba góc trong một tam giác).

Suy ra

$\hat{A}=180°-\widehat{ACB}-\widehat{ABC}=180°-75°-75°=30°$.

Vậy $\widehat{ABC}=\widehat{ACB}=75°$, $\hat{A}=30°.$