Giải SBT Toán 7 trang 65 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 7 trang 65 Tập 2 trong Bài 9: Tính chất ba đường phân giác của tam giác Sách bài tập Toán lớp 7 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 65.

Giải SBT Toán 7 trang 65 Tập 2 Chân trời sáng tạo

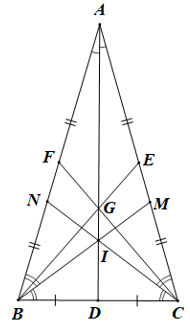
Bài 1 trang 65 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác và gọi I là giao điểm của các đường phân giác của tam giác. Chứng minh ba điểm A, I, G thẳng hàng.

Lời giải:

Vẽ phân giác AD của tam giác ABC.

Xét ∆ABD và ∆ACD có:

AB = AC (do ∆ABC cân tại A),

$\widehat{BAD}=\widehat{CAD}$ (do AD là phân giác của $\widehat{BAC}$),

AD là cạnh chung.

Do đó ∆ABD = ∆ACD (c.g.c)

Suy ra DB = DC.

Khi đó AD vừa là đường phân giác vừa là đường trung tuyến của tam giác ABC.

Mà G là trọng tâm của tam giác và I là giao điểm của các đường phân giác của tam giác ABC.

Suy ra hai điểm I và G đều thuộc AD.

Khi đó ba điểm A, I, G thẳng hàng.

Vậy ba điểm A, I, G thẳng hàng.

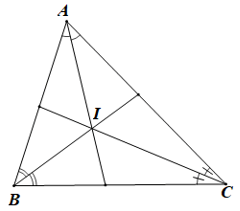
Bài 2 trang 65 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có $\hat{A}=62°$, ba đường phân giác đồng quy tại I. Tính số đo góc BIC.

Lời giải:

Trong ∆CAB có: $\widehat{ACB}+\widehat{ABC}+\widehat{CAB}=180°$ (tổng ba góc trong một tam giác).

Suy ra

$\widehat{ACB}+\widehat{ABC}=180°-\widehat{BAC}=180°-62°=118°$.

Vì BI là phân giác của góc ABC nên $\widehat{IBC}=\frac{\widehat{ABC}}{2}$

Vì CI là phân giác của góc ACB nên $\widehat{ICB}=\frac{\widehat{ACB}}{2}$

Suy ra

$\widehat{IBC}+\widehat{ICB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{118°}{2}=59°$.

Trong ∆CIB có: $\widehat{CIB}+\widehat{IBC}+\widehat{ICB}=180°$ (tổng ba góc trong một tam giác).

Mà $\widehat{IBC}+\widehat{ICB}=59°$ (chứng minh trên)

Suy ra $\widehat{CIB}+59°=180°$

Do đó $\widehat{BIC}=180°-59°=121°$

Vậy $\widehat{BIC}=121°.$

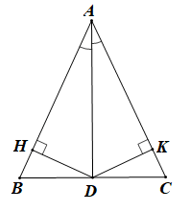
Bài 3 trang 65 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Gọi H và K là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DH = DK.

Lời giải:

Vì AD là phân giác của góc BAC nên $\widehat{BA\text{D}}=\widehat{CA\text{D}}=\frac{\widehat{BAC}}{2}$.

Xét ΔADH và ΔADK có:

$\widehat{AH\text{D}}=\widehat{AKD}\left(=90°\right)$,

AD là cạnh chung,

$\widehat{HA\text{D}}=\widehat{KA\text{D}}$ (chứng minh trên).

Do đó ΔADH = ΔADK (cạnh huyền – góc nhọn).

Suy ra DH = DK (hai cạnh tương ứng).

Vậy DH = DK.

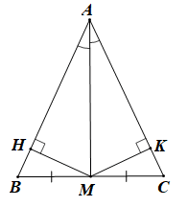
Bài 4 trang 65 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng minh tam giác ABC là tam giác cân.

Lời giải:

Gọi H và K là chân các đường vuông góc kẻ từ M đến AB và AC.

Vì AM là phân giác của góc BAC nên $\widehat{BAM}=\widehat{CAM}=\frac{\widehat{BAC}}{2}$

•Xét ΔAMH và ΔAMK có:

$\widehat{AHM}=\widehat{AKM}\left(=90°\right)$,

AM là cạnh chung,

$\widehat{HAM}=\widehat{KAM}$ (do $\widehat{BAM}=\widehat{CAM}$).

Do đó ΔAMH = ΔAMK (cạnh huyền – góc nhọn).

Suy ra MH = MK (hai cạnh tương ứng).

•Xét ΔBMH và ΔCMK có:

$\widehat{BHM}=\widehat{CKM}\left(=90°\right)$,

BM = CM (do AM là đường trung tuyến của ΔABC),

MH = MK (chứng minh trên).

Do đó ΔBMH = ΔCMK (cạnh huyền – cạnh góc vuông).

Suy ra $\hat{B}=\hat{C}$ (hai góc tương ứng).

Khi đó tam giác ABC cân tại A.

Vậy tam giác ABC cân tại A.