Giải SBT Toán 7 trang 37 Tập 1 Kết nối tri thức

---

Haylamdo sưu tầm và biên soạn Giải SBT Toán 7 trang 37 Tập 1 trong Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 37.

Giải SBT Toán 7 trang 37 Tập 1 Kết nối tri thức

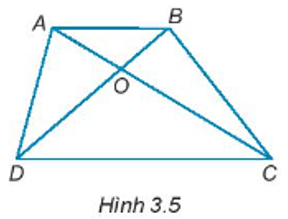
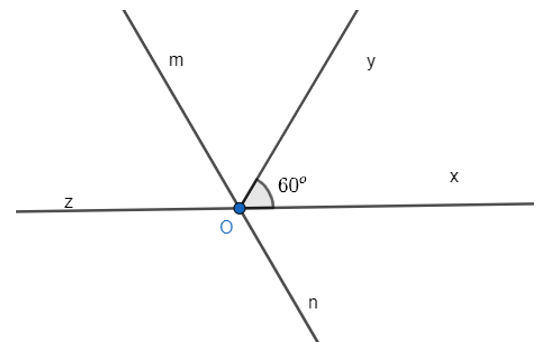
Bài 3.2 trang 37 sách bài tập Toán lớp 7 Tập 1: Cho Hình 3.5

a) Gọi tên các cặp góc đối đỉnh.

b) Gọi tên góc kề bù với $\widehat{AOD}$.

Lời giải:

a) Các cặp góc đối đỉnh là: $\widehat{AOB}$và $\widehat{DOC}$; $\widehat{AOD}$ và $\widehat{BOC}$ .

b) Góc kề bù với góc $\widehat{AOD}$ là góc $\widehat{AOB}$ và $\widehat{COD}$.

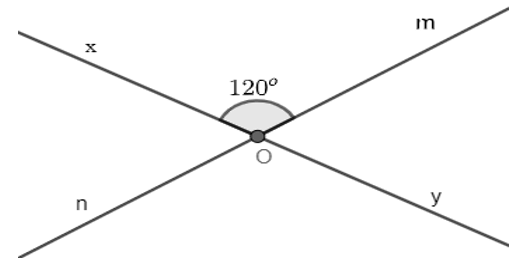
Bài 3.3 trang 37 sách bài tập Toán lớp 7 Tập 1: Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho $\widehat{xOm}=120°$. Tính các góc $\widehat{mOy};\widehat{yOn};\widehat{xOn}.$

Lời giải:

Vì góc $\widehat{xOm}$ và góc $\widehat{nOy}$ là hai góc đối đỉnh nên $\widehat{xOm}$ = $\widehat{nOy}$ =$120°$

Vì góc $\widehat{xOn}$ và góc $\widehat{xOm}$ là hai góc kề bù nên $\widehat{xOn}$ + $\widehat{xOm}$ =$180°$

$\widehat{xOn}+120°$ = $180°$

$\widehat{xOn}$ = $180°-120°$

$\widehat{xOn}= 60°$.

Mà $\widehat{xOn}$ và $\widehat{yOm}$ đối đỉnh nên $\widehat{xOn }= \widehat{yOm}$ = $60°$.

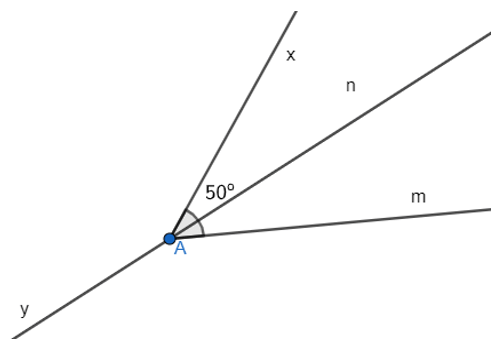
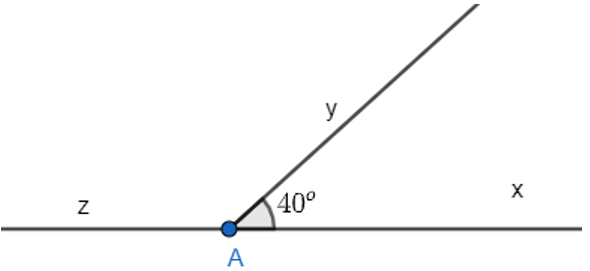
Bài 3.4 trang 37 sách bài tập Toán lớp 7 Tập 1: Vẽ $\widehat{xAm}=50°$. Vẽ tia phân giác An của $\widehat{xAm}$.

a) Tính $\widehat{xAn}$.

b) Vẽ tia Ay là tia đối của tia An. Tính $\widehat{mAy}$.

Lời giải:

a) Vì An là tia phân giác của góc $\widehat{xAm}$ nên $\widehat{xAn}=$ $\widehat{mAn}=\frac{\widehat{xAM}}{2}=\frac{50°}{2}=25°$.

b) Vì tia Ay là tia đối của tia An nên $\widehat{yAn}= 180°$

Do đó, $\widehat{nAm}$ và góc $\widehat{mAy}$ là hai góc kề bù.

Ta có:

$\widehat{nAm}+ \widehat{mAy}$ = 180^o

25^o + $\widehat{mAy}$= 180^o

$\widehat{mAy}$ = 180^o – 25^o

$\widehat{mAy}$ = 155^o.

Vậy $\widehat{mAy}$ = 155^o.

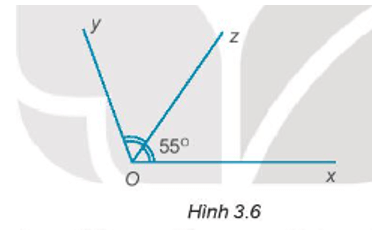
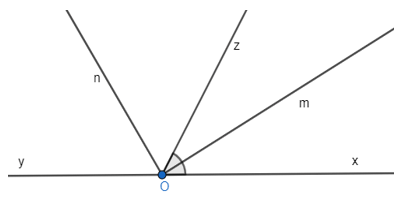
Bài 3.5 trang 37 sách bài tập Toán lớp 7 Tập 1: Cho Hình 3.6. Biết tia Oz là tia phân giác của $\widehat{xOy}$. Tính $\widehat{xOy}$

Lời giải:

Vì Oz là tia phân giác của góc $\widehat{xOy}$ nên $\widehat{xOz} = \widehat{zOy}= \frac{\widehat{xOy}}{2}=55°$.

Do đó, $\widehat{xOy}= 55°.2=110°$.

Vậy $\widehat{xOy}=110°$.

Bài 3.6 trang 37 sách bài tập Toán lớp 7 Tập 1: Vẽ $\widehat{xAy}$ = $40°$. Vẽ $\widehat{yAz}$ là góc kề bù với $\widehat{xAy}$.

Lời giải:

Bài 3.7 trang 37 sách bài tập Toán lớp 7 Tập 1: Cho góc bẹt xOy. Vẽ tia Oz sao cho $\widehat{xOz}=60°$. Vẽ tia Om là tia phân giác của góc xOz. Vẽ tia On là tia phân giác của góc zOy.

a) Tính số đo góc xOm.

b) Tính số đo góc yOn.

c) Tính số đo góc mOn.

Lời giải:

a) Vì Om là tia phân giác của góc $\widehat{xOz}$ nên $\widehat{xOm}=\widehat{mOz}=\frac{\widehat{xOz}}{2}=\frac{60°}{2}=30°$

Vậy $\widehat{xOm}=30°$.

b) Vì góc $\widehat{xOz}$ và $\widehat{yOz}$ là hai góc kề bù nên:

$\widehat{xOz}+\widehat{yOz}$ = 180^o

60^o + $\widehat{yOz}$ = 180⁰

$\widehat{yOz}$ = 180^o – 60⁰

$\widehat{yOz}$ = 120^o

Lại có: On là tia phân giác của góc $\widehat{yOz}$, do đó:

$\widehat{yOn}=\widehat{nOz}=\frac{\widehat{yOz}}{2}=\frac{120°}{2}=60°$

Vậy $\widehat{yOn}=60°$.

c) Ta có: $\widehat{mOn}=\widehat{mOz}+\widehat{zOn}$

$\widehat{mOn}=30°+60° =90°$

Vậy $\widehat{mOn}=90°$.

Bài 3.8 trang 37 sách bài tập Toán lớp 7 Tập 1: Vẽ $\widehat{xOy}=60°$. Vẽ tia Oz là tia đối của tia Ox. Vẽ tia Om là tia phân giác của góc zOy.

a) Tính $\widehat{zOm}$.

b) Vẽ tia On là tia đối của tia Om. Tia Ox có phải là tia phân giác của góc yOn không? Vì sao?

Lời giải:

a) Vì Oz và Ox là hai tia đối nhau nên $\widehat{zOx}=180°$. Do đó, $\widehat{zOy}$ và $\widehat{yOx}$ là hai góc kề bù.

$\widehat{zOy}$ + $\widehat{yOx}$ = 180^o

$\widehat{zOy}$ + 60^o = 180^o

$\widehat{zOy}$ = 180^o – 60^o

$\widehat{zOy}$ = 120^o.

Mà Om là tia phân giác của góc $\widehat{zOy}$ nên ta có:

$\widehat{zOm}=\widehat{mOy}=\frac{\widehat{zOy}}{2}=\frac{120°}{2}=60°$

Vậy $\widehat{zOm}$ = 60^o.

b) Vì On là tia đối của  tia Om và Oz là tia đối của tia Ox nên $\widehat{mOz};\widehat{nOx}$ đối đỉnh.

Suy ra,

$\widehat{mOz}=\widehat{nOx}$ = 60^o.

Ta có: Ox nằm giữa hai tia Oy và On;

$\widehat{xOy}=\widehat{nOx}$ = 60^o.

Do đó, Ox là tia phân giác của góc $\widehat{yOn}$.

Lời giải sách bài tập Toán lớp 7 Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc Kết nối tri thức hay khác:

• Giải SBT Toán 7 trang 36 Tập 1