Giải SBT Toán 7 trang 49 Tập 1 Kết nối tri thức

---

Haylamdo sưu tầm và biên soạn Giải SBT Toán 7 trang 49 Tập 1 trong Ôn tập chương 3 Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 49.

Giải SBT Toán 7 trang 49 Tập 1 Kết nối tri thức

B.Bài tập

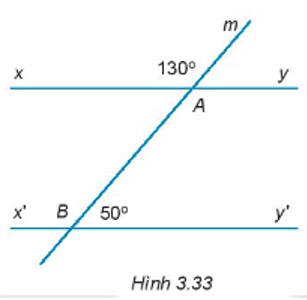
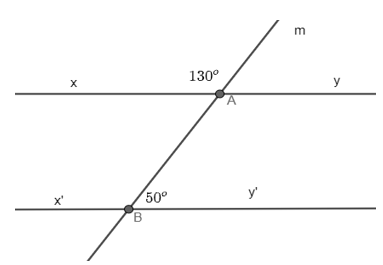
Bài 3.33 trang 49 sách bài tập Toán lớp 7 Tập 1: Cho Hình 3.33. Hãy chứng minh xy // x’y’

Lời giải:

Ta có: $\widehat{mAy}$ và $\widehat{mAx}$ là hai góc kề bù.

Do đó, $\widehat{mAy}+\widehat{mAy}$ = 180^o

Thay số, 130^o + $\widehat{mAy}$ = 180^o.

$\widehat{mAy}$ = 180^o – 130^o = 50^o.

Lại có, $\widehat{mAy}$ và $\widehat{ABy\text{'}}$ là hai góc kề bù và $\widehat{mAy}$ = $\widehat{ABy\text{'}}$ = 50^o.

Do đo, xy // x’y’.

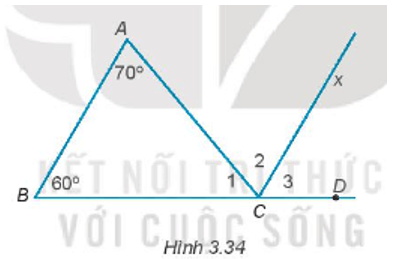
Bài 3.34 trang 49 sách bài tập Toán lớp 7 Tập 1: Cho Hình 3.34. Biết AB // Cx, $\hat{A}=70°$; $\hat{B}=60°$.

Tính số đo các góc ${\hat{C}}_1;{\hat{C}}_2;{\hat{C}}_3$.

Tính số đo các góc ${\hat{C}}_1;{\hat{C}}_2;{\hat{C}}_3$.

Lời giải:

Vì AB song song với Cx nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.

Ta có:

$\hat{B}$ và ${\hat{C}}_3$ là hai góc ở vị trí đồng vị nên $\hat{B}$ = ${\hat{C}}_3$ = 60^o;

$\hat{A}$ và ${\hat{C}}_2$ là hai góc ở vị trí đồng vị nên $\hat{A}$ = ${\hat{C}}_2$ = 70^o;

Ta có: ${\hat{C}}_1+{\hat{C}}_2+{\hat{C}}_3$ = 180^o.

Thay số: ${\hat{C}}_1$+ 70^o + 60^o = 180^o

${\hat{C}}_1$= 180^o – 60^o – 70^o.

${\hat{C}}_1$ = 50^o

Vậy ${\hat{C}}_1$ = 50^o; ${\hat{C}}_2$ = 70^o; ${\hat{C}}_3$ = 60^o.

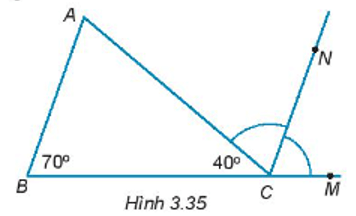
Bài 3.35 trang 49 sách bài tập Toán lớp 7 Tập 1: Cho Hình 3.35. Biết CN là tia phân giác của góc ACM.

a) Chứng minh rằng CN // AB.

b) Tính số đo của góc A.

Lời giải:

a) Ta có: $\widehat{ACB}$ và $\widehat{ACM}$ là hai góc kề bù nên $\widehat{ACB}$ + $\widehat{ACM}$ = 180^o.

Thay số, 40^o + $\widehat{ACM}$ = 180^o

$\widehat{ACM}$ = 180^o – 40^o

$\widehat{ACM}$ = 140^o

Vì CN là tia phân giác của góc $\widehat{ACM}$ nên $\widehat{ACN}=\widehat{NCM}=\frac{\widehat{ACM}}{2}=\frac{140}{2}=70°$

Ta có: $\widehat{NCM}$ và $\hat{B}$ ở vị trí đồng vị và $\widehat{NCM}=\hat{B}=70°$.

Do đó, AB song song CN.

b) Vì AB song song với CN nên các cặp góc so le trong sẽ bằng nhau và các cặp góc đồng vị sẽ bằng nhau.

Ta có: $\hat{A}$ và $\widehat{ACN}$ là hai góc so le trong. Do đó, $\widehat{ACN}$ = $\hat{A}$ = 70^o.

Vậy $\hat{A}$ = 70^o.

Lời giải sách bài tập Toán lớp 7 Ôn tập chương 3 Kết nối tri thức hay khác:

• Giải SBT Toán 7 trang 47 Tập 1

• Giải SBT Toán 7 trang 48 Tập 1

• Giải SBT Toán 7 trang 50 Tập 1