Giải SBT Toán 7 trang 62 Tập 1 Kết nối tri thức
Haylamdo sưu tầm và biên soạn Giải SBT Toán 7 trang 62 Tập 1 trong Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 62.
Giải SBT Toán 7 trang 62 Tập 1 Kết nối tri thức
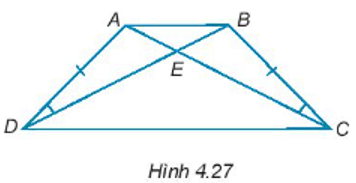
Bài 4.27 trang 62 sách bài tập Toán lớp 7 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng AD = BC, . Chứng minh rằng:
a) .
b) ∆AED = ∆BEC.
c) AB song song với DC.
Lời giải:
a) Xét tam giác AED có:
(1)
Xét tam giác BEC có:
(2)
Mà (hai góc đối đỉnh) (3)
Từ (1); (2); (3) suy ra, hay (điều phải chứng minh).
b) Xét ∆AED và ∆BEC ta có:
(chứng minh trên)
(giả thiết)
AD = CB (giả thiết)
Do đó, ∆AED = ∆BEC (g – c – g).
c) Vì ∆AED = ∆BEC nên AE = BE; ED = EC.
Ta có: AC = AE + EC; BD = BE + ED.
Do đó, AC = BD.
Xét ∆ABD và ∆BAC ta có:
AC = BD (chứng minh trên)
AB chung
AD = CB (giả thiết)
Do đó, ∆ABD = ∆BAC (c – c – c)
Suy ra (hai góc tương ứng)
Xét tam giác AEB có:
Do đó, (vì do )
Suy ra (4)
Xét ∆ACD và ∆BDC ta có:
AC = BD (chứng minh trên)
CD chung
AD = CB (giả thiết)
Do đó, ∆ACD = ∆BDC (c – c – c)
Suy ra (hai góc tương ứng)
Xét tam giác DEC có:
Do đó, (vì do = )
Suy ra (5)
Lại có, là hai góc đối đỉnh nên (6)
Từ (4); (5); (6) suy ra = hay .
Mà hai góc này lại ở vị trí so le trong nên AB // CD.
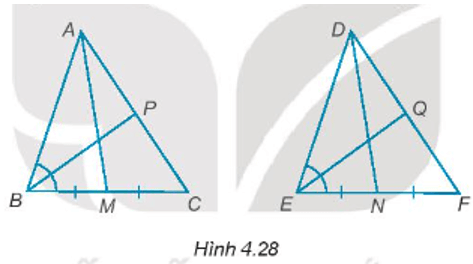
Bài 4.28 trang 62 sách bài tập Toán lớp 7 Tập 1: Cho tam giác ABC bằng tam giác DEF (H.4.28).
a) Gọi M và N lần lượt là trung điểm các đoạn thẳng BC và EF. Chứng minh rằng AM = DN.
b) Trên hai cạnh AC và DF lấy hai điểm P và Q sao cho BP, EQ lần lượt là phân giác của các góc và . Chứng minh rằng: BP = EQ.
Lời giải:
a) Vì ∆ABC = ∆DEF nên
Vì M là trung điểm của BC nên BM = MC = .
Vì N là trung điểm của EF nên EN = NF = .
Mà BC = EF (chứng minh trên) nên BM = EN.
Xét ∆ABM và ∆DEN ta có:
BM = EN (chứng minh trên)
AB = DE (chứng minh trên)
(do chứng minh trên)
Do đó, ∆ABM = ∆DEN (c – g – c).
Suy ra, AM = DN (hai cạnh tương ứng).
b) Vì BP là tia phân giác của góc nên =
Vì EQ là tia phân giác của góc nên
Mà = nên = .
Xét ∆PBC và ∆QEF ta có:
BC = EF (chứng minh trên)
(chứng minh trên)
(do chứng minh trên)
Do đó, ∆PBC = ∆QEF (g – c – g)
Suy ra, BP = EQ (hai cạnh tương ứng).
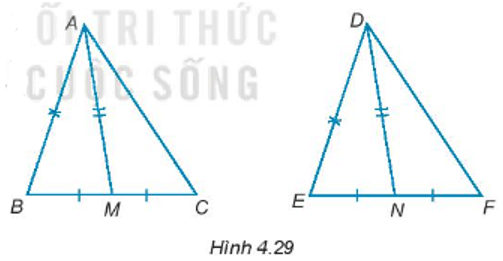
Bài 4.29 trang 62 sách bài tập Toán lớp 7 Tập 1: Gọi M và N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và DEF. Giả sử rằng AB = DE, BC = EF, AM = DN (H.4.29). Chứng minh rằng ∆ABC = ∆DEF.
Lời giải:
Vì M là trung điểm của BC nên BM = MC =
Vì N là trung điểm của EF nên EN = NF =
Mà BC = EF (giả thiết) nên BM = EN.
Xét ∆ABM và ∆DEN ta có:
AB = DE (giả thiết)
BM = EN (chứng minh trên)
AM = DN (giả thiết)
Do đó, ∆ABM = ∆DEN (c – c – c).
Suy ra, (hai góc tương ứng) hay .
Xét ∆ABC và ∆DEF ta có:
AB = DE (giả thiết)
BC = EF (giả thiết)
(chứng minh trên)
Do đó, ∆ABC = ∆DEF (c – g – c).
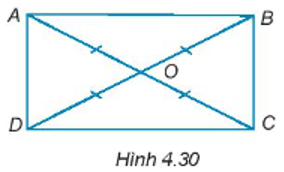
Bài 4.30 trang 62 sách bài tập Toán lớp 7 Tập 1: Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như Hình 4.30. Chứng minh ABCD là hình chữ nhật.
Lời giải:
Xét ∆OAB và ∆OCD ta có:
OA = OC (giả thiết)
(hai góc đối đỉnh)
OB = OD (giả thiết)
Do đó, ∆OAB = ∆OCD (c – g – c).
Suy ra AB = DC và hay .
Mà hai góc này ở vị trí so le trong, do đó AB // DC (1).
Xét ∆OAD và ∆OCB ta có:
OA = OC (giả thiết)
(hai góc đối đỉnh)
OD = OB (giả thiết)
Do đó, ∆OAD = ∆OCB (c – g – c).
Suy ra AD = BC và hay .
Mà hai góc này ở vị trí so le trong nên AD // BC (2).
Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành.
Ta có: OA = OC = OB = OD, AC = OA + OC, BD = OB + OD.
Do đó, AC = BD.
Xét tam giác ABD và tam giác DCA có:
AB = DC (chứng minh trên)
AD: cạnh chung
BD = AC (chứng minh trên)
Do đó, ∆ABD = ∆DCA (c – c – c).
Suy ra .
Lại có: (do AB // DC, hai góc ở vị trí trong cùng phía)
Do đó: .
Vậy hình bình hành ABCD có một góc vuông nên nó là hình chữ nhật.
Lời giải sách bài tập Toán lớp 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Kết nối tri thức hay khác: