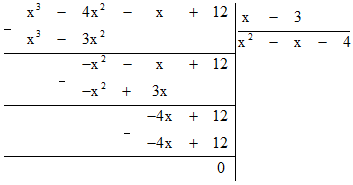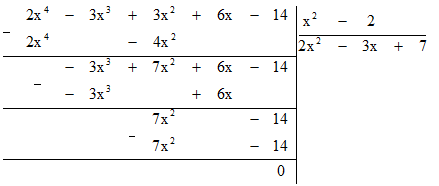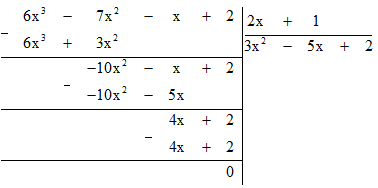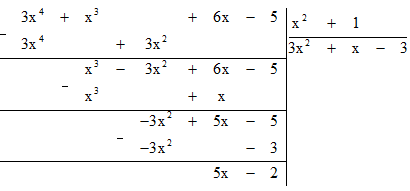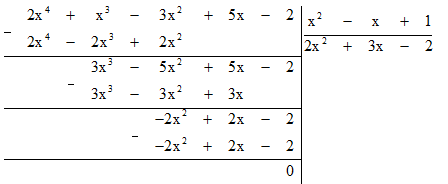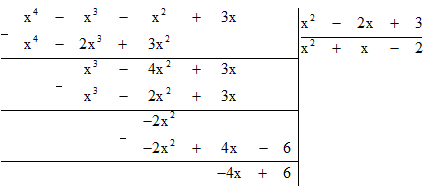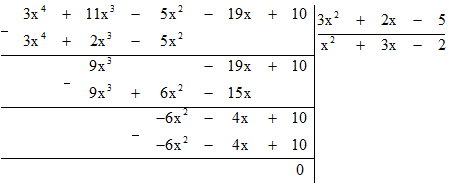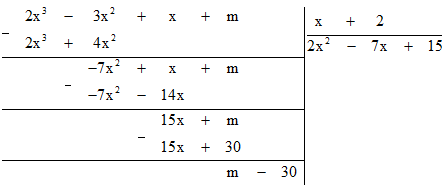Giải SBT Toán 7 trang 34 Tập 2 Kết nối tri thức

---

Haylamdo sưu tầm và biên soạn Giải SBT Toán 7 trang 34 Tập 2 trong Bài 28: Phép chia đa thức một biến Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 34.

Giải SBT Toán 7 trang 34 Tập 2 Kết nối tri thức

Bài 7.25 trang 34 sách bài tập Toán lớp 7 Tập 2: Tìm số tự nhiên n sao cho đa thức 1,2x⁵ − 3x⁴ + 3,7x² chia hết cho xⁿ.

Lời giải:

Đa thức đã cho chia hết cho xⁿ nếu từng hạng tử của nó chia hết cho xⁿ, nói riêng là 3,7x² chia hết cho xⁿ. Điều này xảy ra khi n ≤ 2.

Mà n là số tự nhiên nên n ∈ {0; 1; 2}.

Vậy n ∈ {0; 1; 2} thỏa mãn yêu cầu bài toán.

Bài 7.26 trang 34 sách bài tập Toán lớp 7 Tập 2: Thực hiện các phép chia sau:

a) (−4x⁵ + 3x³ − 2x²) : (−2x²);

b) (0,5x³− 1,5x² + x) : 0,5x;

c) (x³ + 2x² − 3x + 1) : $\frac{1}{3}$x².

Lời giải:

a) (−4x⁵ + 3x³ − 2x²) : (−2x²)

= (−4x⁵) : (−2x²) + (3x³): (−2x²)+ (−2x²) : (−2x²)

= 2x³ − 1,5x + 1

b) (0,5x³− 1,5x² + x) : 0,5x

= 0,5x³ : 0,5x + (−1,5x²) : 0,5x + x : 0,5x

= x² − 3x + 2

c) (x³ + 2x² − 3x + 1) : $\frac{1}{3}$x²

Ta có thể viết : x³ + 2x² − 3x + 1 = (3x + 6)$\frac{1}{3}$x² + (−3x + 1)

Do đa thức – 3x + 1 có bậc là 1, nhỏ hơn bậc 2 của đa thức chia nên đẳng thức này chứng tỏ 3x + 6 là thương và – 3x + 1 là dư trong phép chia đã cho.

Bài 7.27 trang 34 sách bài tập Toán lớp 7 Tập 2: Đặt tính và làm phép chia sau:

a. (x³ − 4x² − x + 12) : (x − 3)

b. (2x⁴ − 3x³ + 3x² + 6x − 14) : (x² − 2)

Lời giải:

a) (x³ − 4x² − x + 12) : (x − 3)

Vậy kết quả của phép chia(x³ − 4x² − x + 12) : (x − 3) bằng x² − x − 4.

b) (2x⁴ − 3x³ + 3x² + 6x − 14) : (x² − 2)

Vậy kết quả phép chia(2x⁴ − 3x³ + 3x² + 6x − 14) : (x² − 2) bằng 2x² −3x + 7

Bài 7.28 trang 34 sách bài tập Toán lớp 7 Tập 2: Khi làm phép chia (6x³ − 7x² − x + 2) : (2x + 1) , bạn Quỳnh cho kết quả đa thức dư là 4x + 2.

a) Không làm phép chia, hãy cho biết bạn Quỳnh đúng hay sai, tại sao?

b) Tìm thương và dư trong phép chia đó.

Lời giải:

a) Quỳnh sai. Vì bậc của đa thức dư, nếu khác 0, phải nhỏ hơn bậc của đa thức chia.

b) (6x³ − 7x² − x + 2) : (2x + 1)

Vậy thương của phép chia (6x³ − 7x² − x + 2) : (2x + 1) bằng 3x² − 5x + 2 dư 0.

Bài 7.29 trang 34 sách bài tập Toán lớp 7 Tập 2: Cho hai đa thức A = 3x⁴ + x³ + 6x −5 và B = x² + 1. Tìm thương Q và dư R trong phép chia A cho B rồi kiểm nghiệm lại rằng A = BQ + R.

Lời giải:

Thực hiện phép chia (3x⁴ + x³ + 6x −5) : (x² + 1)

Vậy phép chia (3x⁴ + x³ + 6x −5) : (x² + 1) có thương Q = 3x² + x − 3 và dư R = 5x − 2

Kiểm nghiệm BQ + R = (x² + 1)(3x² + x − 3) + 5x − 2

= x²( 3x² + x − 3) + 1. (3x² + x − 3) + 5x − 2

= 3x⁴ + x³− 3x² + 3x² + x − 3 + 5x − 2

= 3x⁴ + x³+ (−3x² + 3x²) + (x + 5x) + (−3 − 2)

= 3x⁴ + x³ + 6x −5 = A

Bài 7.30 trang 34 sách bài tập Toán lớp 7 Tập 2: Thực hiện các phép chia sau:

a) (2x⁴ + x³ − 3x² + 5x − 2) : (x² − x + 1)

b) (x⁴ − x³ − x² + 3x) : (x² − 2x +3)

Lời giải:

a)(2x⁴ + x³ − 3x² + 5x − 2) : (x² − x + 1)

Vậy phép chia(2x⁴ + x³ − 3x² + 5x − 2) : (x² − x + 1) có thương là 2x² + 3x − 2.

b) (x⁴ − x³ − x² + 3x) : (x² − 2x +3)

Vậy phép chia(x⁴ − x³ − x² + 3x) : (x² − 2x +3) có thương là x²+ x − 2 và dư −4x + 6.

Bài 7.31 trang 34 sách bài tập Toán lớp 7 Tập 2: Cho đa thức A(x) = 3x⁴ + 11x³ − 5x² − 19x − 5 . Tìm đa thức H(x) sao cho:

A(x) = (3x² + 2x − 5).H(x)

Lời giải:

Ta có A(x) = (3x² + 2x − 5).H(x)

H(x) = A(x) : (3x² + 2x − 5) = (3x⁴ + 11x³ − 5x² − 19x − 5) : (3x² + 2x − 5)

Vậy H(x) = x² + 3x − 2.

Bài 7.32 trang 34 sách bài tập Toán lớp 7 Tập 2: Tìm số m sao cho đa thức P(x) = 2x³ – 3x² + x + m chia hết cho đa thức x + 2.

Lời giải:

Thực hiện phép chia P(x) : (x + 2)

Để phép chia này là phép chia hết thì m − 30 = 0.

Vậy m = 30.

Bài 7.33 trang 34 sách bài tập Toán lớp 7 Tập 2: Cho đa thức P(x). Chứng minh rằng:

a) Nếu P(x) chia hết cho x – a thì a là một nghiệm của đa thức P(x).

b) Nếu x = a là một nghiệm của đa thức P(x) thì P(x) chia hết cho x – a.

Lời giải:

a) Giả sử P(x) chia hết cho x – a. Gọi Q(x) là đa thức thương, ta có:

P(x) = (x − a)Q(x) (1)

Từ đẳng thức (1), ta có P(a) = (a − a)Q(a) = 0.

Vậy a là một nghiệm của P(x).

b) Ngược lại, cho a là một nghiệm của P(x). Giả sử chia P(x) cho x – a, ta được thương là Q(x) và dư là R(x), nghĩa là ta có:

P(x) = (x – a)Q(x) + R(x) (2)

Trong đó hoặc R(x) = 0, hoặc nếu R(x) ≠ 0 thì R(x) phải có bậc nhỏ hơn bậc của đa thức x – a, tức là nhỏ hơn 1.

Sau đây, ta sẽ chứng tỏ rằng chỉ có thể xảy ra R(x) = 0.

Thật vậy, nếu R(x) ≠ 0 thì do bậc của R(x) nhỏ hơn 1 nên R(x) có bậc 0. Nói cách khác, R(x) là một số khác 0 nào đó. Nhưng điều đó là vô lí vì khi đó đẳng thức (2) không thể xảy ra, chẳng hạn khi x = a thì vế trái bằng 0 trong khi vế phải khác 0.

Vậy chỉ có thể xảy ra R(x) = 0, nghĩa là P(x) chia hết cho x – a.