Cho tam giác GIK như Hình 6 SBT Toán 8

Giải SBT Toán 8 Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số - Cánh diều

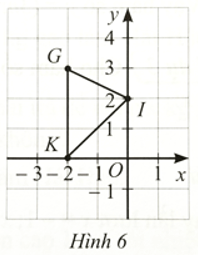
Bài 14 trang 55 SBT Toán 8 Tập 1: Cho tam giác GIK như Hình 6.

a) Xác định toạ độ các điểm G, I, K.

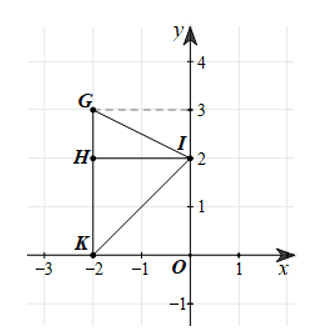
b) Xác định toạ độ điểm H để tứ giác KOIH là hình vuông.

c) Ba điểm G, H, K có thẳng hàng hay không? Vì sao?

d) Tính tỉ số $\frac{G H}{H K}$ .

Lời giải:

Cho tam giác GIK như Hình 6 SBT Toán 8

Từ điểm G kẻ đường thẳng song song với trục Ox, cắt Oy tại 3, kẻ đường thẳng song song với Oy cắt Ox tại ‒2. Do đó tọa độ điểm G là: G(‒2; 3).

Điểm I nằm trên trục Oy có tung độ là 2 nên có hoành độ là 0. Do đó tọa độ điểm I là: I(0; 2).

Điểm K nằm trên trục Ox có hoành độ là ‒2 nên có hoành độ là 0. Do đó tọa độ điểm K là: K(‒2; 0).

b) Do K, I lần lượt nằm trên Ox, Oy nên OK ⊥ OI.

Mặt khác OK = OI = 2 (đơn vị độ dài)

Từ I kẻ đường thẳng song song với OK, từ K kẻ đường thẳng song song với OI, hai đường thẳng này cắt nhau tại điểm H (‒2; 2) cần tìm.

Thật vậy, do IH // OK và KH // OI nên KOIH là hình bình hành.

Lại có OI = OK nên KOIH là hình thoi.

Mà $\hat{I O K} = 90 °$ nên KOIH là hình vuông.

Vậy điểm H có tọa độ là H(–2; 2).

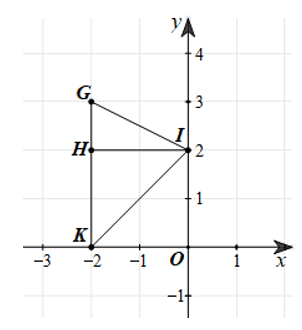
Cho tam giác GIK như Hình 6 SBT Toán 8

c) G, H, K điểm thẳng hàng vì ba điểm đều thuộc đường thẳng đi qua điểm ‒2 trên trục Ox và vuông góc với trục Ox.

d) Ta có: HK = 2 và GH = 3 – 2 = 1

Suy ra $\frac{G H}{H K} = \frac{1}{2}$ .

Lời giải SBT Toán 8 Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số hay khác: