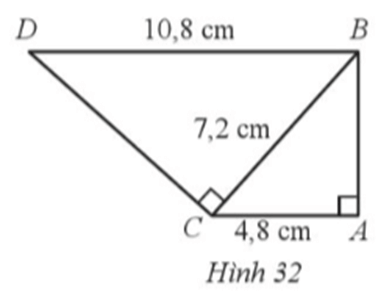
Quan sát Hình 32 có góc BAC = 90 độ, góc BCD = 90 độ, DB = 10,8 cm, BC = 7,2 cm

Quan sát có , , DB = 10,8 cm, BC = 7,2 cm và CA = 4,8 cm. Chứng minh ∆DBC ᔕ ∆BCA.

Giải SBT Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác - Cánh diều

Bài 36 trang 72 SBT Toán 8 Tập 2: Quan sát Hình 32 có $\widehat{BAC}=90°$, $\widehat{BCD}=90°$, DB = 10,8 cm, BC = 7,2 cm và CA = 4,8 cm. Chứng minh ∆DBC ᔕ ∆BCA.

Lời giải:

Nhận thấy: $\frac{DB}{CB}=\frac{10,8}{7,2}=\frac{3}{2}, \frac{BC}{CA}=\frac{7,2}{4,8}=\frac{3}{2}$

Do đó $\frac{DB}{CB}=\frac{BC}{CA}=\frac{3}{2}.$

Xét ∆DBC và ∆BCA có:

$\widehat{BCD}=\widehat{CAB}=90°$ và $\frac{DB}{CB}=\frac{BC}{CA}$

Suy ra ∆DBC ᔕ ∆BCA (cạnh huyền và cạnh góc vuông tương ứng tỉ lệ).

Vậy ∆DBC ᔕ ∆BCA.

Lời giải SBT Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác hay khác:

• Bài 31 trang 72 SBT Toán 8 Tập 2: Tam giác thứ nhất có độ dài các cạnh là: 2,6 cm; 7,1 cm; 8 cm. Tam giác thứ hai có độ dài các cạnh là: 7,8 cm; 21,3 cm; 24 cm. Hỏi hai tam giác đó có đồng dạng không? Vì sao? ....

• Bài 32 trang 72 SBT Toán 8 Tập 2: Tam giác ABC có độ dài các cạnh là AB = 9 cm, AC = 7 cm, BC = 15 cm. Tam giác MNP đồng dạng với tam giác ABC ....

• Bài 33 trang 72 SBT Toán 8 Tập 2: Biết tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số đồng dạng là k. Hỏi tỉ số chu vi của tam giác ABC và tam giác A’B’C’ bằng bao nhiêu? ....

• Bài 34 trang 72 SBT Toán 8 Tập 2: Cho tứ giác ABCD có AB = 27 cm, BC = 9 cm, BD = 8 cm, AD = 24 cm và DB² = AD.CD. Hỏi DB có thể là tia phân giác của góc ADC hay không? Vì sao? ....

• Bài 35 trang 72 SBT Toán 8 Tập 2: Cho tam giác IKH và tam giác I’K’H’ có $\widehat{IKH}=90°$, $\widehat{KHI}=60°$, $\widehat{I^{\text{'}}{K}^{\text{'}}{H}^{\text{'}}}=90°$, $\widehat{K^{\text{'}}{I}^{\text{'}}{H}^{\text{'}}}=30°$. Chứng minh: ∆I’K’H’ ᔕ ∆IKH. ....