Cho tam giác ABC vuông tại A, có đường phân giác AD. Vẽ hình vuông MNPQ ở đó M
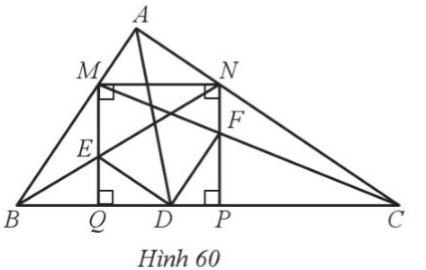
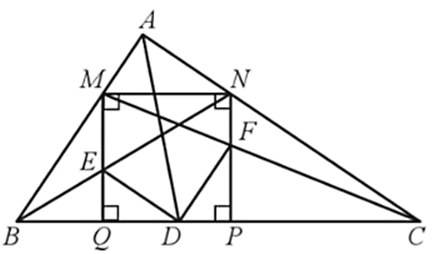
Cho tam giác ABC vuông tại A, có đường phân giác AD. Vẽ hình vuông MNPQ ở đó M thuộc cạnh AB, N thuộc cạnh AC, P và Q thuộc cạnh BC. Gọi E và F lần lượt là giao điểm của BN và MQ, CM và NP (). Chứng minh:
Giải SBT Toán 8 Bài tập cuối chương 8 - Cánh diều
Bài 73 trang 85 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A, có đường phân giác AD. Vẽ hình vuông MNPQ ở đó M thuộc cạnh AB, N thuộc cạnh AC, P và Q thuộc cạnh BC. Gọi E và F lần lượt là giao điểm của BN và MQ, CM và NP (Hình 60). Chứng minh:
a) DE song song với AC;
b) DE = DF.
Lời giải:
a) Do MNPQ là hình vuông nên MQ // NP, mà E ∈ MQ nên EQ // NP.
Xét ∆BNP với EQ // NP, ta có (định lí Thalès) (1)
MNPQ là hình vuông nên MQ ⊥ BC, do đó tam giác BQM vuông tại Q.
Xét ∆BQM (vuông tại Q) và ∆BAC (vuông tại A) có: là góc chung
Do đó ∆BQM ᔕ ∆BAC (g.g).
Suy ra (tỉ số đồng dạng)
Hay mà QM = QP (do MNPQ là hình vuông)
Do đó (2)
Xét ∆ABC có AD là phân giác của góc BAC nên: (tính chất đường phân giác) (3)
Từ (1), (2), (3) ta có
Xét ∆NBC có nên DE // NC (định lí Thalès đảo) hay DE // AC.
b) Do DE // AC (câu a) nên (hệ quả của định lí Thalès)
Do đó
• Do MNPQ là hình vuông nên MQ // NP, mà F ∈ NP nên FP // MQ.
Xét ∆MQB với FP // MQ, ta có (định lí Thalès) (4)
Xét ∆CPN (vuông tại P) và ∆CAB (vuông tại A) có: là góc chung
Do đó ∆CPN ᔕ ∆CAB (g.g).
Suy ra (tỉ số đồng dạng) hay
Mà PQ = PN (do MNPQ là hình vuông) nên (5)
Từ ta có (6)
Từ (4), (5), (6) ta có
Xét ∆MBC có nên DF // BM (định lí Thalès đảo) hay DF // AB.
Suy ra (hệ quả của định lí Thalès), nên .
Mặt khác, ∆ABC với MN // BC (cùng vuông góc với MQ), ta có (hệ quả của định lí Thalès), do đó
Lại có nên = =
Suy ra DE = DF.
Lời giải SBT Toán 8 Bài tập cuối chương 8 hay khác:
Bài 59 trang 83 SBT Toán 8 Tập 2: Cho ∆MNP ᔕ ∆M’N’P’ và . Số đo góc P là: ....
Bài 60 trang 83 SBT Toán 8 Tập 2: Hình 54 cho biết A’B’ = 4, A’O = 3, AO = 6, OB = x, AB = y ....
Bài 61 trang 83 SBT Toán 8 Tập 2: Cho tam giác ABC có DE // BC (Hình 55) ....