Giải SBT Toán 8 trang 20 Tập 1 Cánh diều

---

Haylamdo biên soạn và sưu tầm với giải sách bài tập Toán 8 trang 20 Tập 1 trong Bài tập cuối chương 1 SBT Toán 8 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 trang 20.

Giải SBT Toán 8 trang 20 Tập 1 Cánh diều

Bài 35 trang 20 SBT Toán 8 Tập 1: Phân tích mỗi đa thức sau thành nhân tử:

a) $3x^2-\sqrt{3}x+\frac{1}{4}$;

b) x² – x – y² + y;

c) x³ + 2x² + x – 16xy².

Lời giải:

a) $3x^2-\sqrt{3}x+\frac{1}{4}={\left(\sqrt{3}x\right)}^2-2.\sqrt{3}x.\frac{1}{2}+{\left(\frac{1}{2}\right)}^2={\left(\sqrt{3}x-\frac{1}{2}\right)}^2$.

b) x² – x – y² + y

= (x² ‒ y²) ‒ (x ‒ y)

= (x ‒ y)(x + y) ‒ (x ‒ y)

= (x ‒ y)(x + y ‒ 1).

c) x³ + 2x² + x – 16xy²

= x(x² + 2x + 1 ‒ 16y²)

= x[(x² + 2x + 1) ‒ 16y²]

= x[(x + 1)² ‒ (4y)²]

= x(x + 1 ‒ 4y)(x + 1 + 4y).

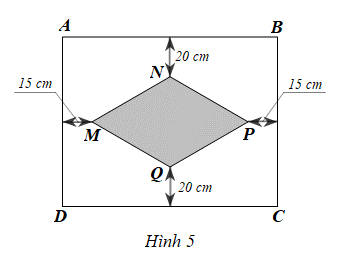
Bài 36 trang 20 SBT Toán 8 Tập 1: Một chiếc khăn trải bàn có dạng hình chữ nhật ABCD được thêu một hoạ tiết có dạng hình thoi MNPQ ở giữa với MP = x (cm), NQ = y (cm) (x > y > 0) như Hình 5.

Viết đa thức biểu thị diện tích phần còn lại của chiếc khăn trải bàn đó.

Lời giải:

Diện tích của chiếc khăn trải bàn là:

(15 + x + 15)(20 + y + 20)

= (x + 30)(y + 40) = xy + 40x + 30y + 1200 (cm²)

Diện tích của phần hoạ tiết là: $\frac{1}{2}xy$ (cm²)

Đa thức biểu thị diện tích phần còn lại của chiếc khăn trải bàn đó là:

$xy+40x+30y+1200-\frac{1}{2}xy=\frac{1}{2}xy+40x+30y+1200$(cm²).

Bài 37* trang 20 SBT Toán 8 Tập 1: Tìm số tự nhiên n để n³ – n² + n – 1 là số nguyên tố.

Lời giải:

Ta có:n³ – n² + n – 1

= (n³ ‒ n²) + (n ‒ 1)

= n²(n ‒ 1) + (n ‒ 1)

= (n ‒ 1)(n² + 1).

Với mọi số tự nhiên n, ta có: n ‒ 1 < n² + 1.

Do đó, để n³ – n² + n – 1 là số nguyên tố thì n ‒ 1 = 1 nên .

Khi đó n³ – n² + n – 1 = 5 là số nguyên tố.

Vậy n = 2 thoả mãn yêu cầu của đề bài.

Lời giải SBT Toán 8 Bài tập cuối chương 1 hay khác:

• Giải SBT Toán 8 trang 18 Tập 1

• Giải SBT Toán 8 trang 19 Tập 1